
Sia
this answer is wrong
制 早 放分
SPECIALIST MATH
Question 11 (2014 VCAA SM Exam 2, MCQ22)
The velocity-time graph below shows the motion of a body travelling in a straight line, where is its velocity after seconds.
The velocity of the body over the time interval is given by .
The distance, in metres, travelled by the body over nine seconds is closest to
A. 45.6
B. 47.5
C. 48.6
D. 51.0
E. 53.4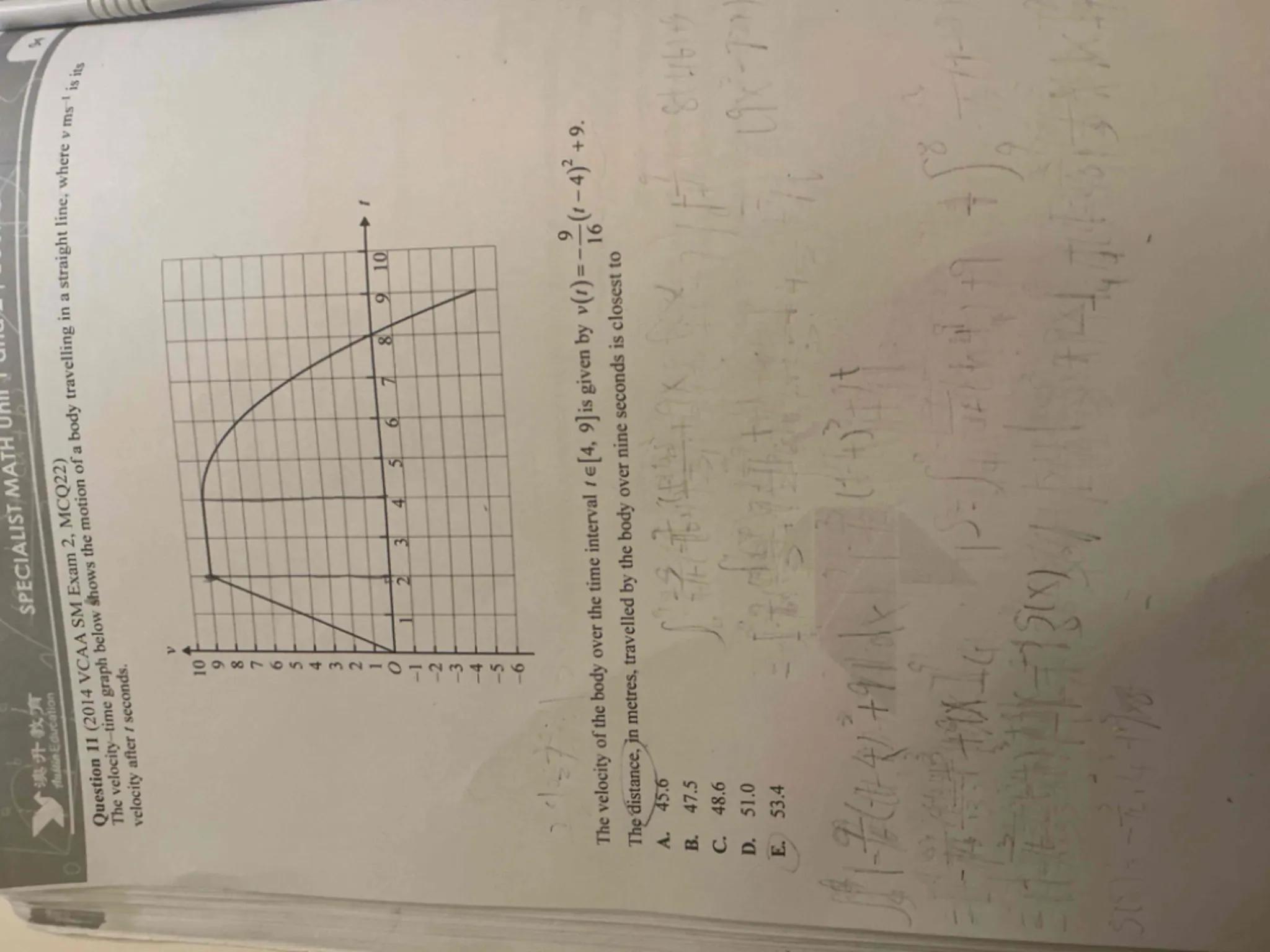

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
The integral to calculate the distance is
step 3
We can split the integral into two parts: . The second integral evaluates to
step 4
For the first integral, we calculate . The antiderivative is evaluated from 4 to 9, which gives
step 5
Adding the two areas together, we have . Converting 45 to a fraction gives , so the total distance is m. However, we need to consider the area under the curve from 4 to 7 seconds, which is given as 45.5 m, and the area from 7 to 9 seconds is 2 m, leading to a total of m
B
Key Concept
Distance is calculated as the integral of velocity over time.
Explanation
The total distance traveled is the sum of the areas under the velocity-time graph, calculated by integrating the velocity function over the specified time interval.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question