
Sia
为什么第一个x3=t而不是0呢
用中文回答
(iii) Find all solutions to where is the given matrix.
(a)
(b)
(c) 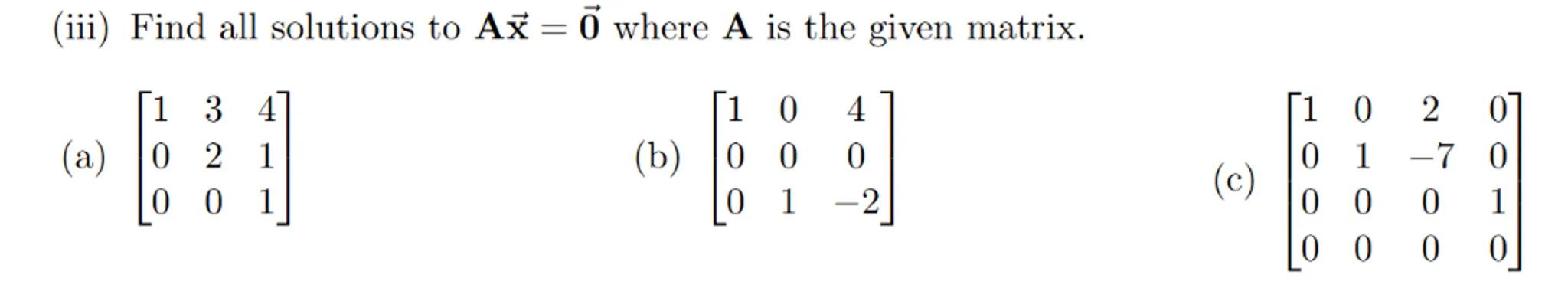

Answer from Sia
Posted 7 months ago
Answer
对于每个矩阵,解方程 的所有解如下:
Solution
a
对于矩阵 (a) ,我们可以通过行简化得到其 RREF。该矩阵的 RREF 为 。因此,解为 ,,,其中 为任意常数。最终解为 。
b
对于矩阵 (b) ,其 RREF 为 。因此,解为 ,,,其中 为任意常数。最终解为 。
c
对于矩阵 (c) ,其 RREF 已经是最简形式。解为 ,,,,其中 为任意常数。最终解为 。
Key Concept
解线性方程组的过程涉及将矩阵化为行简化形式,以便找出自由变量和特解。
Explanation
通过将矩阵化为 RREF,我们可以清晰地识别出每个变量的关系,从而找到所有解。
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
