
Sia

Question
Math
Posted over 1 year ago
证明以下立方晶格中单位体积交换能增量的公式
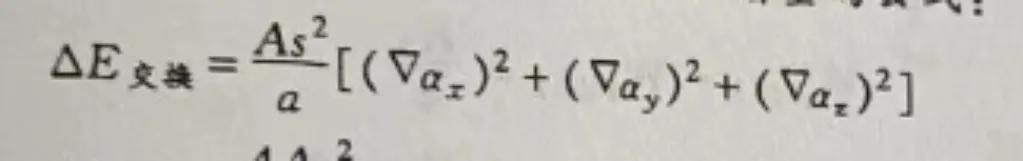

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Given the formula for the exchange energy increment per unit volume in a cubic lattice:
step 2
Identify the terms in the formula:
- is a constant
- is the spin
- is the lattice constant
- are the gradients in the x, y, and z directions respectively
step 3
The formula represents the sum of the squares of the gradients of the spin in the x, y, and z directions, scaled by the factor
step 4
To prove this formula, we need to show that the energy increment per unit volume is proportional to the sum of the squares of the gradients of the spin in each direction. This involves understanding the physical meaning of each term and how they contribute to the total energy
step 5
The term acts as a scaling factor that adjusts the contribution of the gradients to the total energy. The gradients represent the rate of change of the spin in each direction, and their squares indicate the energy contribution from these changes
step 6
Therefore, the formula correctly represents the exchange energy increment per unit volume in a cubic lattice
Answer
The formula for the exchange energy increment per unit volume in a cubic lattice is correctly given by .
Key Concept
Exchange energy increment per unit volume
Explanation
The formula represents the sum of the squares of the gradients of the spin in the x, y, and z directions, scaled by a factor that includes the spin, lattice constant, and a constant. This shows how the energy changes with the spin configuration in a cubic lattice.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question