
Sia
1. For how many integers with is the expression equal to an integer?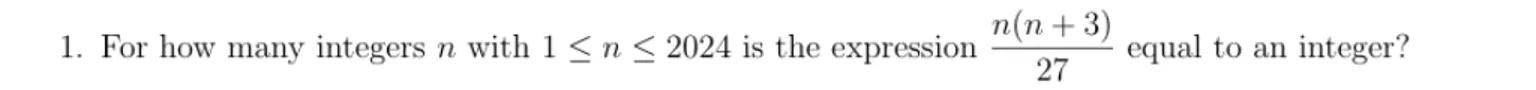

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
We need to determine for how many integers with the expression is an integer
step 2
For to be an integer, must be divisible by 27
step 3
We need to find the values of such that
step 4
This means or must be divisible by 27
step 5
Let's consider the two cases separately:
1.
2.
step 6
For the first case, where is an integer. The range gives . Solving for , we get . So, there are 74 values of in this case
step 7
For the second case, where is an integer. This gives . The range gives . Solving for , we get or . This simplifies to . So, there are 75 values of in this case
step 8
However, we must exclude the overlap where is both and . This happens when , or , which is not possible for integer and . Therefore, there is no overlap
step 9
Adding the two cases, we get values of for which is an integer
Answer
149
Key Concept
Divisibility by 27
Explanation
To determine when is an integer, we need to be divisible by 27. This occurs when either or is a multiple of 27.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
