
Sia

Question
Math
Posted almost 2 years ago
10. Let be an matrix with positive real eigenvalues . Let be an eigenvector belonging to for each , and let .
(a) Show that .
(b) Show that if , then .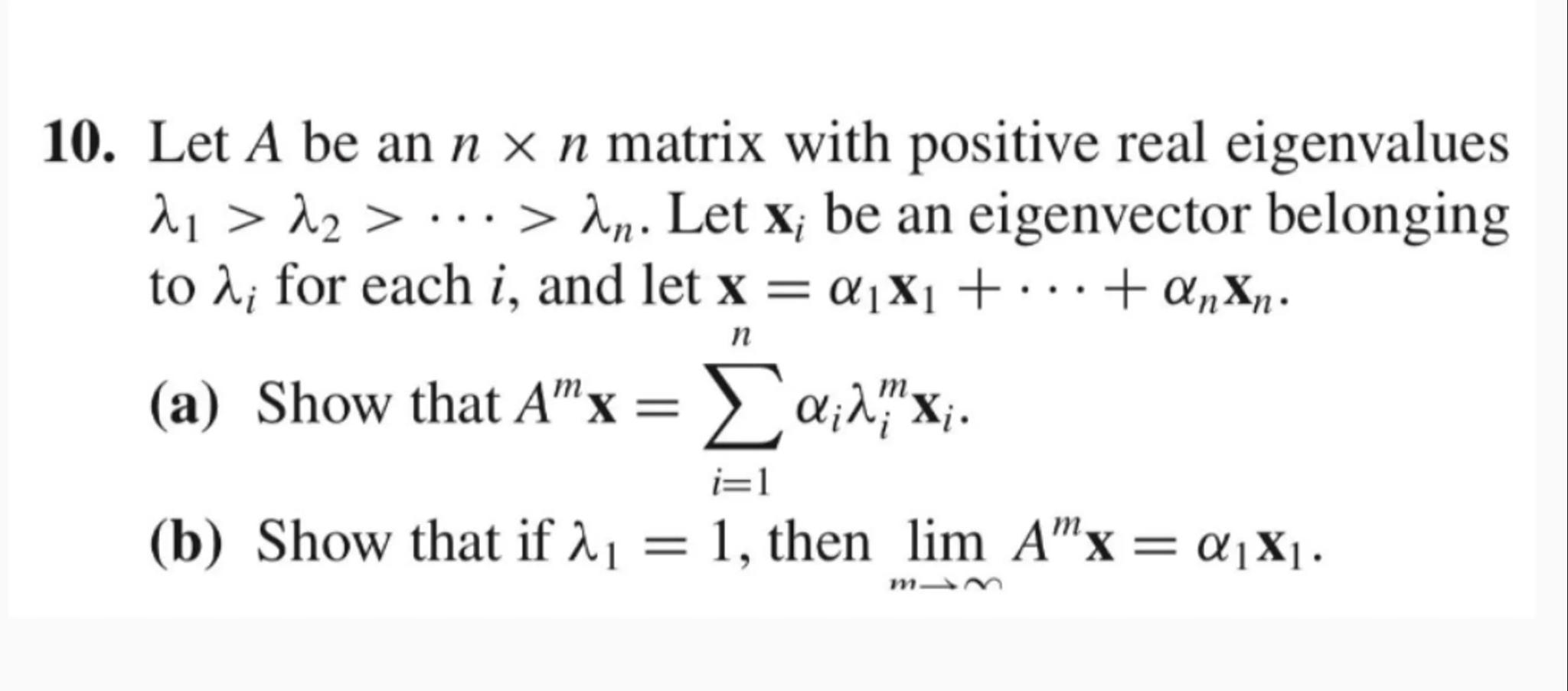

Answer from Sia
Posted almost 2 years ago
Solution by Steps
step 1
Given the matrix with positive real eigenvalues and corresponding eigenvectors , we need to show that
step 2
Since is an eigenvector of corresponding to eigenvalue , we have
step 3
Applying repeatedly, we get
step 4
Given , we apply to both sides:
step 5
Using linearity of , we get
step 6
Substituting , we obtain
step 7
Therefore,
step 8
For part (b), if , we need to show that
step 9
From part (a),
step 10
As , for all since
step 11
Therefore,
step 12
Since , for all
step 13
Thus,
Answer
Key Concept
Eigenvalues and Eigenvectors
Explanation
The solution leverages the properties of eigenvalues and eigenvectors, particularly how powers of a matrix act on its eigenvectors, and the behavior of eigenvalues less than 1 as their powers increase.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question