
Sia
14 A sportsman hits a ball with a bat.
The ball leaves the bat at a speed of at an angle of to the horizontal, as shown.
Calculate the horizontal distance travelled by the ball before returning to the height it was hit from.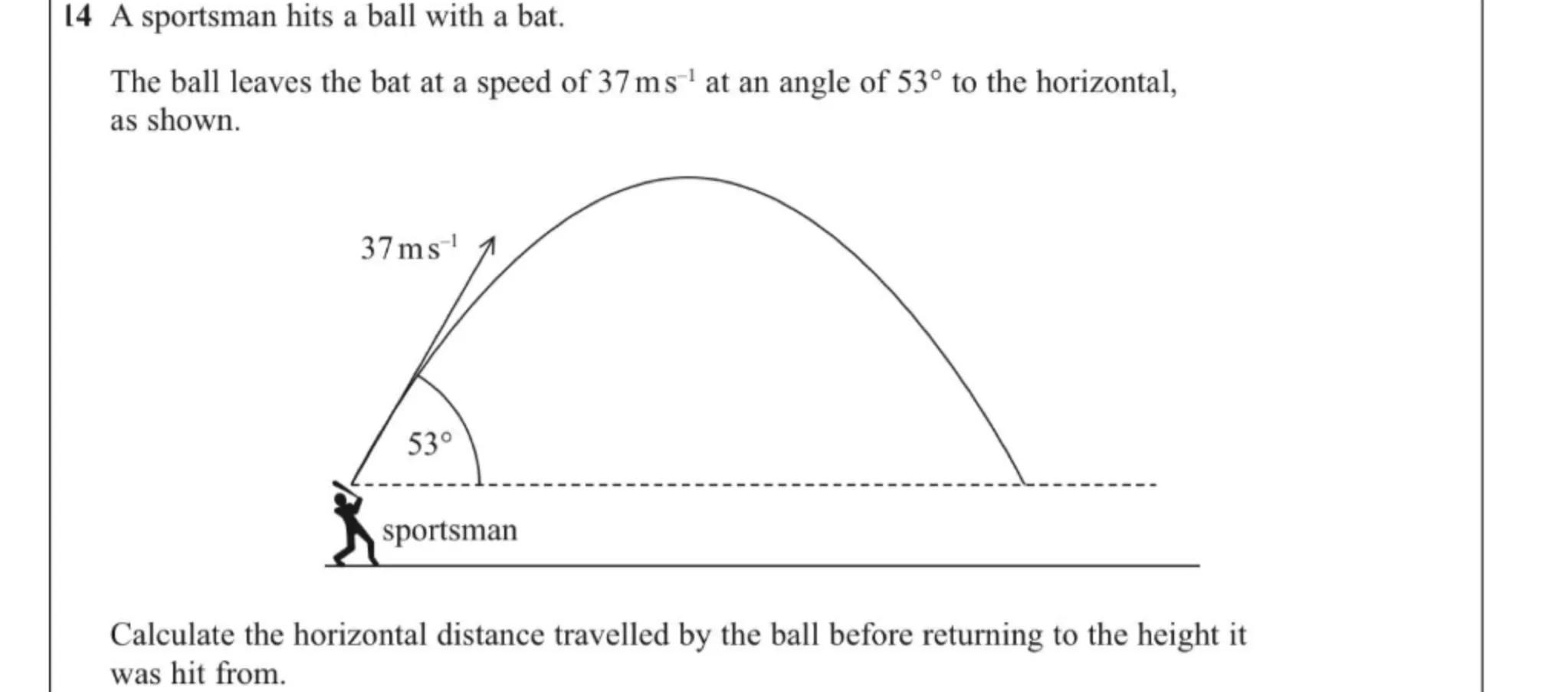

Answer from Sia
Posted over 1 year ago
Solution
a
First, we need to resolve the initial velocity into its horizontal and vertical components. The horizontal component is given by: . Calculating this gives us:
b
The vertical component of the initial velocity is: . This results in:
c
To find the time of flight, we can use the formula for the vertical motion. The time to reach the maximum height is given by: . The total time of flight is then:
d
The horizontal distance traveled (range) can be calculated using:
Answer
134.9 m
Key Concept
Projectile Motion: The motion of an object thrown into the air, subject to the acceleration due to gravity. The horizontal and vertical motions are independent of each other. Key equations include: for horizontal distance and for total time of flight.
Explanation
By resolving the initial velocity into horizontal and vertical components and using the equations of motion, we can determine the total horizontal distance traveled by the ball before it returns to its original height.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question