
Sia
I) In the circuit shown, the cells have negligible internal resistance and the reading on the galvanometer is zero.
What is the value of resistor ?
A
B
C
D 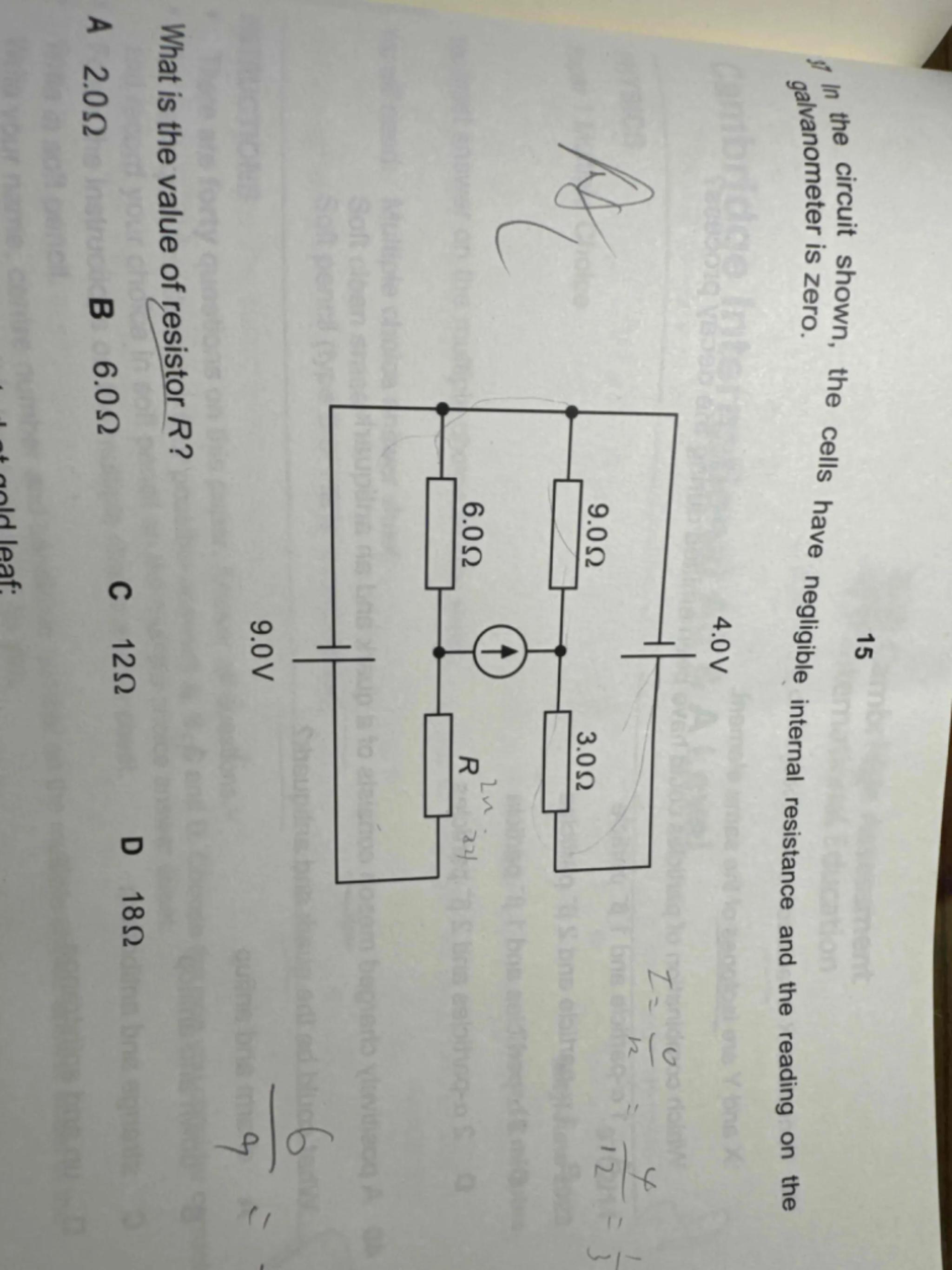

Answer from Sia
Posted over 1 year ago
Solution
a
Given that the reading on the galvanometer is zero, the potential difference across the galvanometer must be zero. This implies that the potential at the point where the galvanometer is connected is the same for both loops
b
Apply Kirchhoff's Voltage Law (KVL) to the left loop:
c
Apply Kirchhoff's Voltage Law (KVL) to the right loop:
d
Since the potential at the galvanometer connection point is the same for both loops, the current in the right loop must be the same as in the left loop:
e
Substitute into the right loop equation:
f
The closest value to 3.67Ω among the given options is 6.0Ω
Answer
B
Key Concept
Kirchhoff's Voltage Law (KVL): The sum of the electrical potential differences (voltage) around any closed network is zero.
Explanation
By applying KVL to both loops and using the condition that the galvanometer reading is zero, we can determine the value of the unknown resistor .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
