
Sia
22.23 10月20日国日
thepageschool.instructure.com
Canvas Student
En
那开
240910 1: > Assignments > Unit 4 Homework ,
Home
Sylitous
Modules
Grades
Submission Details
Grade:
Unit 4 Homework
Cecilia Guo submitted Oct 21 at 12:18pm
Add a Comment:
Opaints caned
A 2 kg object traveling at on a frictionless horizontal surface col-Ides head-on with and sticks to a 3 kg object initially at rest. Which of the following correctly identifes the change in total kinetic energy and the resulting speed of the objects after the collision? 5 P149
Media Comment
Attach File
Save
\begin{tabular}{|c|c|}
\hline Kinetic Energy & Speed \\
\hline Increases & \\
\hline
\end{tabular}
\begin{tabular}{|c|c|}
\hline Kinetic Energy & Speed \\
\hline Decreases & \\
\hline
\end{tabular}
\begin{tabular}{|c|c|}
\hline Kinetic Energy & Speed \\
\hline Increases & \\
\hline
\end{tabular}
\begin{tabular}{|c|c|c|c|}
\hline \multirow{3}{*}{} & \multirow[t]{3}{*}{O} & & \\
\hline & & Kinetic Energy & Speed \\
\hline & & Decreases & \\
\hline
\end{tabular}
22 23 10月20日国日
-
thepageschool.instructure.com
Canvas Student
En
那开
240910 1: > Assignments > Unit 4 Homework ,
Home
Syltats
Modules
Grades
Submission Details
Grade:
Unit 4 Homework
Cecilia Guo submitted Oct 21 at 12:18pm
Add a Comment:
4
65
4)
Media Comment
Attach File
5
Opoints earned
Save
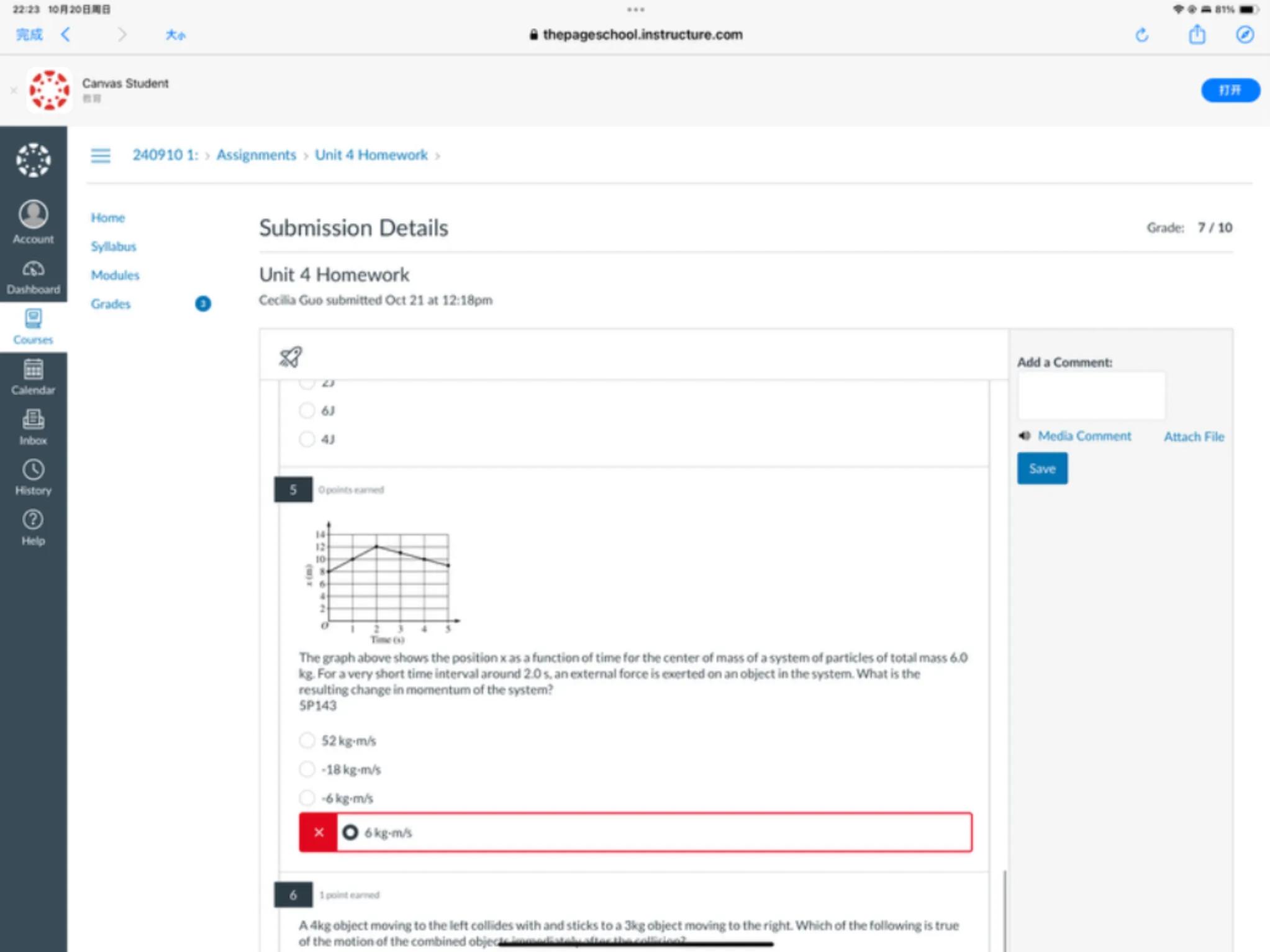
The graph above shows the position x as a function of time for the center of mass of a system of particles of total mass 6.0 kg. For a very short time interval around 2.0 s , an external force is exerted on an object in the system. What is the resulting change in momentum of the system? SP143
6
1 point earred
A 4 kg object moving to the left collides with and sticks to a 3 kg object moving to the right. Which of the following is true of the motion of the combined object
22.23 10月20日用田
thepageschool.instructure.com
Canvas Student
En
那开
240910 1: > Assignments > Unit 4 Homework >
Home
5yluthos
Modules
Grades
2
Opolits earsed
Grade:
Submission Details
Unit 4 Homework
Cecilia Guo submitted Oct 21 at 12:18pm
Add a Comment:
Media Comment
Attach File
Save
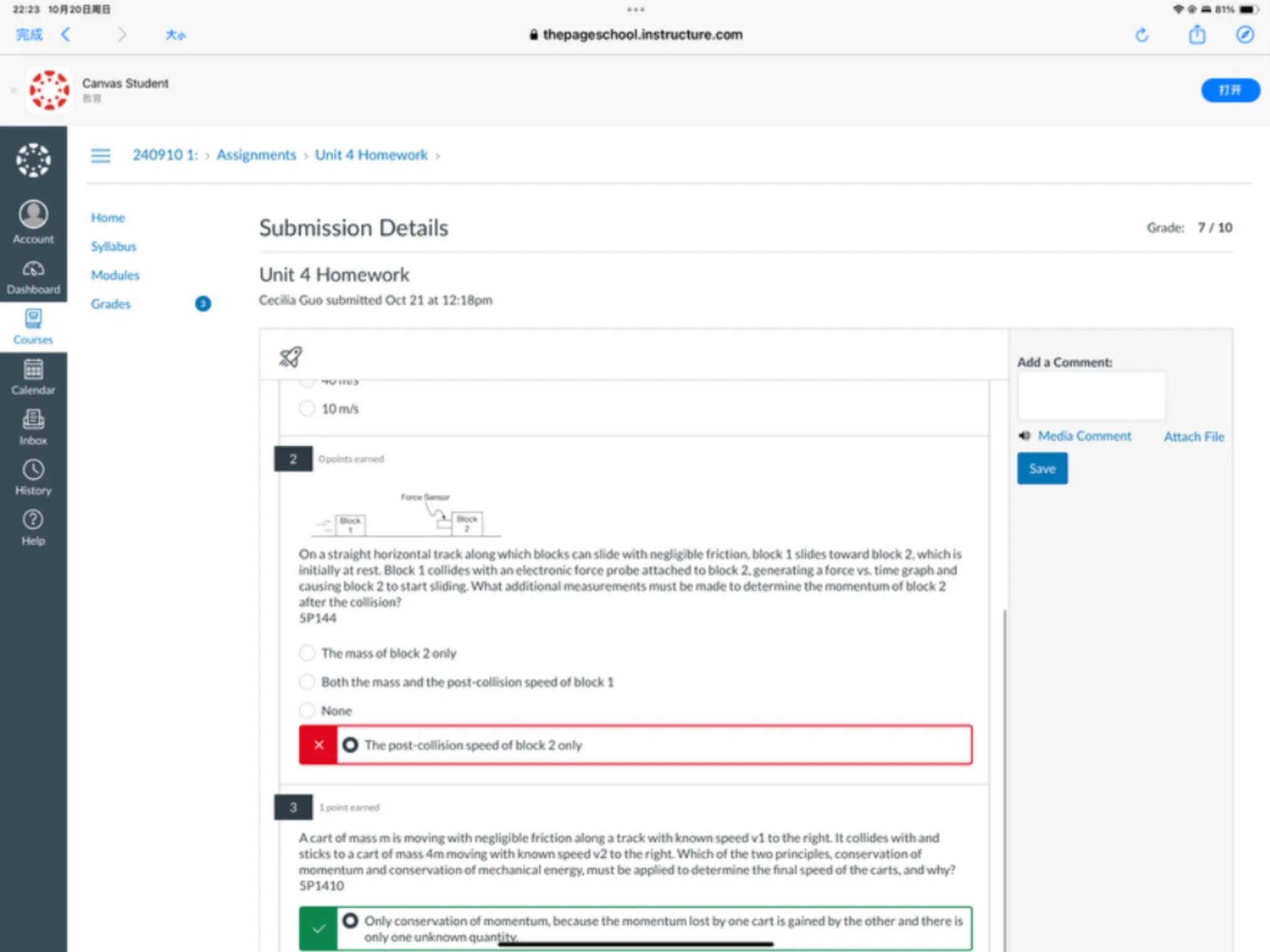
On a straight horizontal track along which blocks can slide with negligible friction. block 1 slides toward block 2, which is initially at rest. Block 1 collides with an electronic force probe attached to block 2 . generating a force vs. time graph and causing block 2 to start sliding. What additional measurements must be made to determine the momentum of block 2 after the collision? SP144
The mass of block 2 only
Both the mass and the post-collision speed of block 1
None
The post-collision speed of block 2 only
3
1 point earned
Acart of mass is moving with negligible friction along a track with known speed to the right. It collides with and sticks to a cart of mass 4 m moving with known speed to the right. Which of the two principles, conservation of momentum and conservation of mechanical energy, must be applied to determine the final speed of the carts, and why? 5P1410
O Only conservation of momentum, because the momentum lost by one cart is gained by the other and there is only one unknown quantify.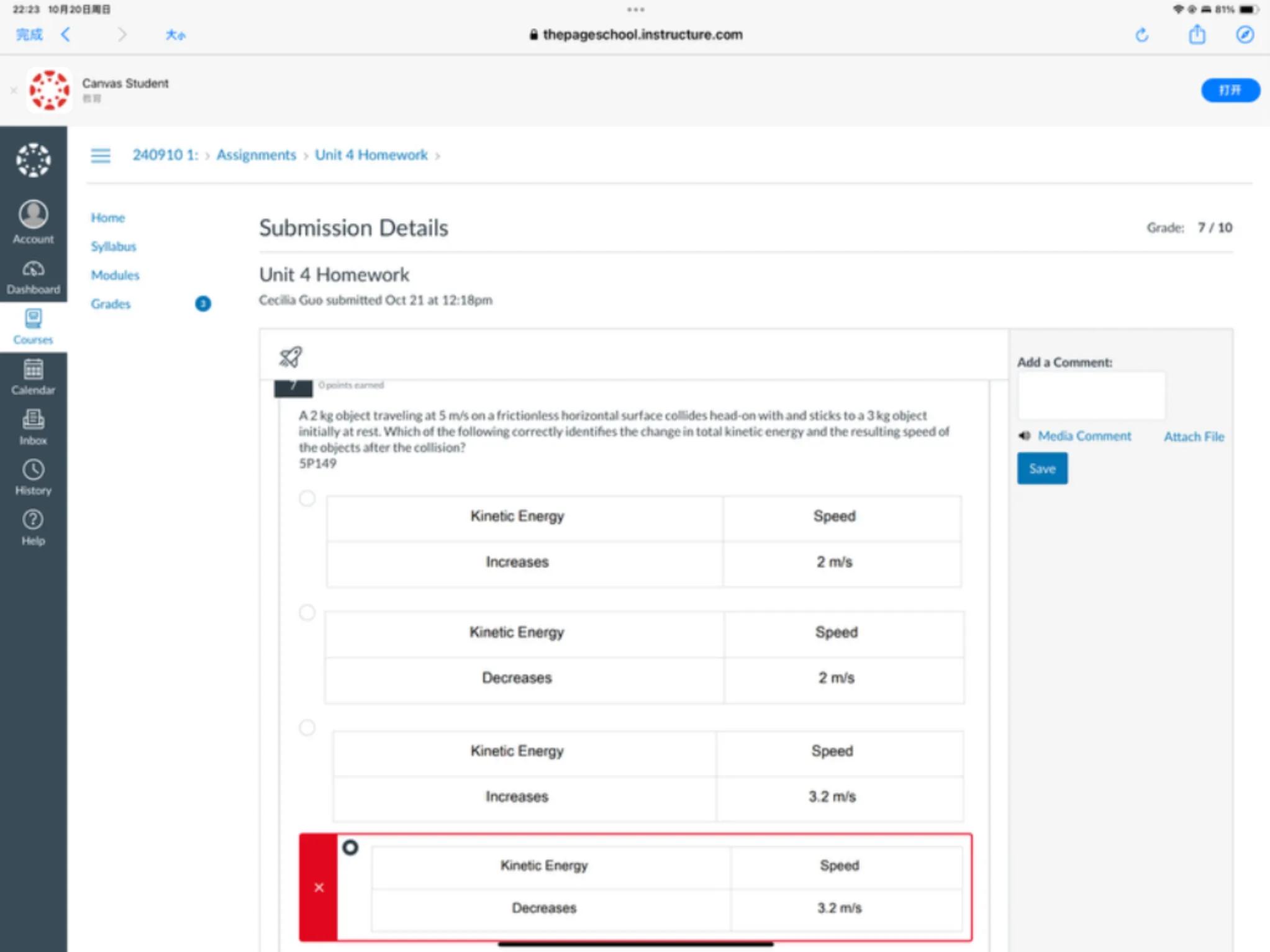

Answer from Sia
Posted 5 months ago
Solution
a
To find the final speed after the collision, we apply the conservation of momentum. The initial momentum of the system is given by: where , , , and \(v_2 = 0 \, \text{m/s}$$. Thus, $$p_{initial} = (2 \, \text{kg})(5 \, \text{m/s}) + (3 \, \text{kg})(0) = 10 \, \text{kg m/s}$$
b
After the collision, the two objects stick together, so we can denote their combined mass as . The final momentum is equal to the initial momentum: . Setting the initial and final momenta equal gives us: , which simplifies to
c
To find the change in kinetic energy, we calculate the initial and final kinetic energies. The initial kinetic energy is: . The final kinetic energy after the collision is: . The change in kinetic energy is: , indicating a decrease in kinetic energy
Answer
D
Key Concept
Conservation of Momentum: The total momentum of a closed system remains constant if no external forces act on it. The equation is . Kinetic Energy: The energy of motion, given by .
Explanation
In this collision, momentum is conserved, leading to a final speed of 2 m/s, while kinetic energy decreases due to the inelastic nature of the collision.
\)Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question