
Sia
28. A 20 kg beam is supported by a cable as shown in the diagram below.
a. Find the tension in the cable supporting the beam.
b. Find the magnitude of the force exerted by the wall on the beam.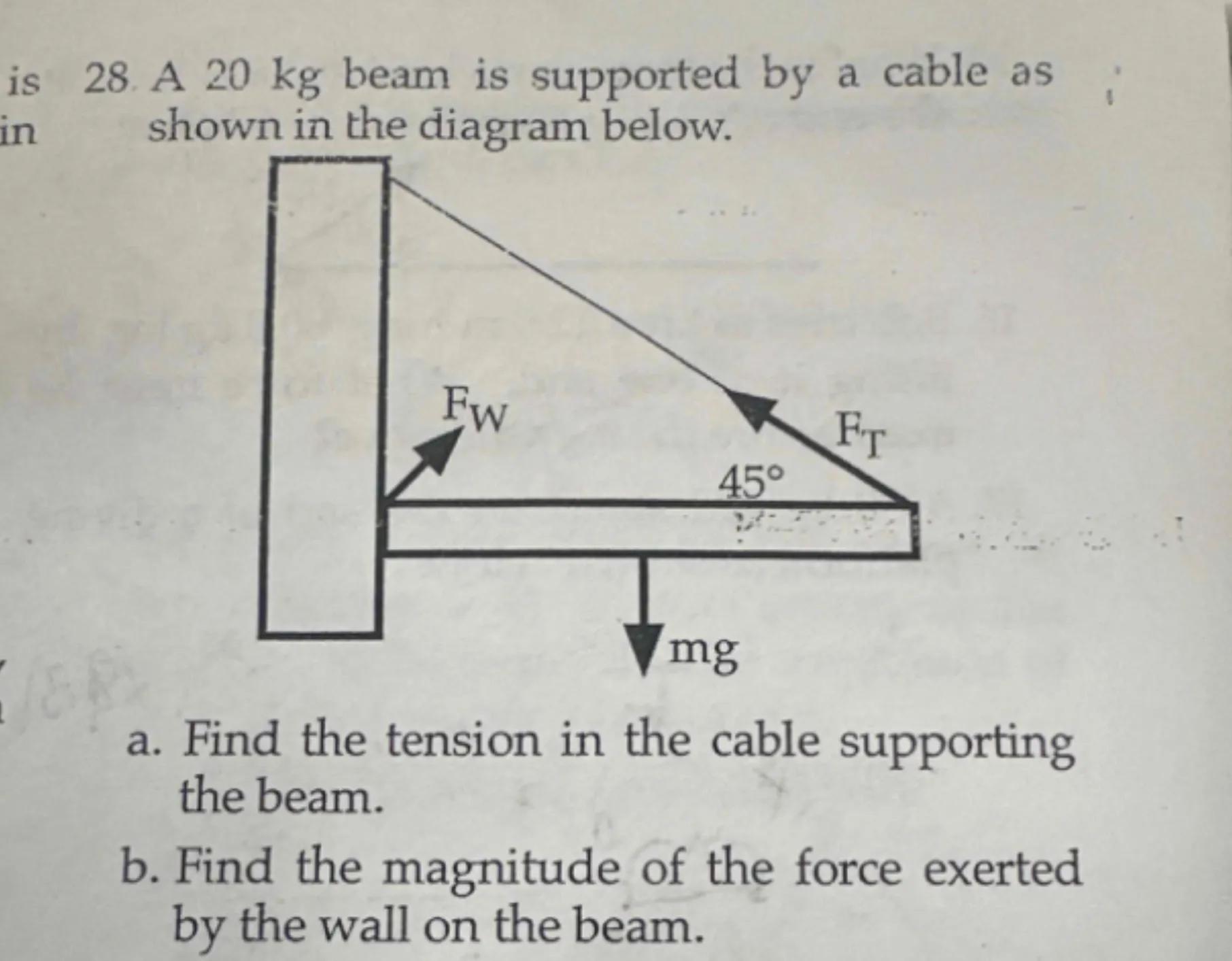

Answer from Sia
Posted about 1 year ago
Solution
a
To find the tension in the cable, we first analyze the forces acting on the beam. The weight of the beam is given by acting downwards. The beam is in static equilibrium, so the sum of the vertical forces must equal zero. The vertical component of the tension can be expressed as . Therefore, we have the equation: . Substituting the values, we get: . Solving for gives us
b
To find the force exerted by the wall on the beam, we need to consider the horizontal forces. The horizontal component of the tension is given by . Since the beam is in equilibrium, the force exerted by the wall, , must balance this horizontal component:
Answer
Tension in the cable: approximately 277.1 N; Force exerted by the wall: 196.2 N
Key Concept
Static Equilibrium: In static equilibrium, the sum of all forces and the sum of all torques acting on an object must be zero. This leads to equations that can be solved to find unknown forces.
Explanation
By applying the conditions of static equilibrium, we can determine the tension in the cable and the force exerted by the wall on the beam. The calculations show how the forces balance out in both vertical and horizontal directions.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
