
Sia
2)
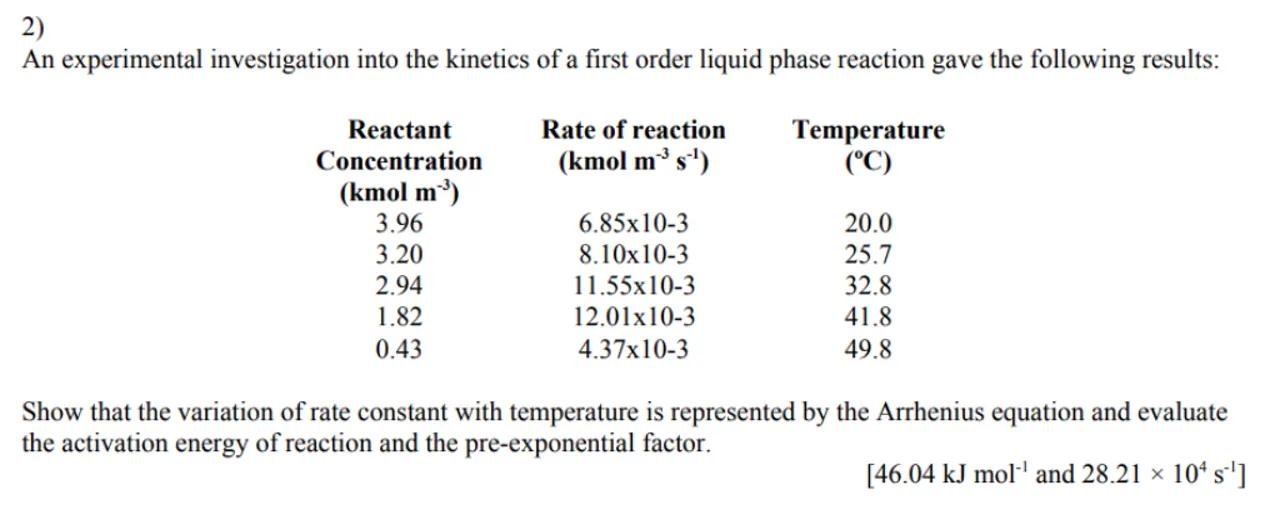
An experimental investigation into the kinetics of a first order liquid phase reaction gave the following results:
\begin{tabular}{ccc}
\begin{tabular}{c}
Reactant \\
Concentration \\
\end{tabular} & \begin{tabular}{c}
Rate of reaction \\
\end{tabular} & \begin{tabular}{c}
Temperature \\
\end{tabular} \\
3.96 & & \\
3.20 & & 20.0 \\
2.94 & & 25.7 \\
1.82 & & 32.8 \\
0.43 & & 41.8 \\
& & 49.8
\end{tabular}
Show that the variation of rate constant with temperature is represented by the Arrhenius equation and evaluate the activation energy of reaction and the pre-exponential factor.

Answer from Sia
Posted over 1 year ago
Solution
1
Understand the Arrhenius equation: The Arrhenius equation relates the rate constant of a reaction to the temperature (in Kelvin), the activation energy , and the pre-exponential factor . It is given by , where is the gas constant (8.314 J mol K)
2
Linear form of the Arrhenius equation: To evaluate the activation energy and the pre-exponential factor, we use the linear form of the Arrhenius equation: . A plot of versus should yield a straight line with a slope of and an intercept of
3
Convert temperatures to Kelvin and calculate $\ln(k)$: Convert each temperature from degrees Celsius to Kelvin by adding 273.15. Then, calculate the natural logarithm of each rate constant
4
Plot and determine slope and intercept: Plot versus to determine the slope and intercept. The slope will give , and the intercept will give
5
Calculate $E_a$ and $A$: Use the slope to calculate the activation energy by multiplying the slope by . Then, exponentiate the intercept to find the pre-exponential factor
Answer
The activation energy is 46.04 kJ mol and the pre-exponential factor is s.
Key Concept
The Arrhenius equation relates the rate constant of a reaction to the temperature, activation energy, and pre-exponential factor.
Explanation
By plotting the natural logarithm of the rate constant against the inverse of the temperature in Kelvin, we can determine the activation energy and pre-exponential factor from the slope and intercept of the resulting line.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
