
Sia
3. [-/1 Points]
DETAILS
MY NOTES
SESSCALCET2 6.1.011.MI.
ASK YOUR TEACHER
PRACTICE ANOTHER
Evaluate the integral. (Use for the constant of integration.)
Need Help?
Read It
Watch it
Master it
Submit Answer
4. Points]
DETAILS
MY NOTES
SESSCALCET2 6.1.013.MI.
ASK YOUR TEACHER
PRACTICE ANOTHER
Evaluate the integral. (Use for the constant of integration.)
Need Help?
Read It
Watch it
Master II
Submit Answer
5. [-/1 Points]
DETAILS
MY NOTES
SESSCALCET2 6.1.021.
ASK YOUR TEACHER
PRACTICE ANOTHER
Evaluate the integral.
Need Help?
Read It
Watch it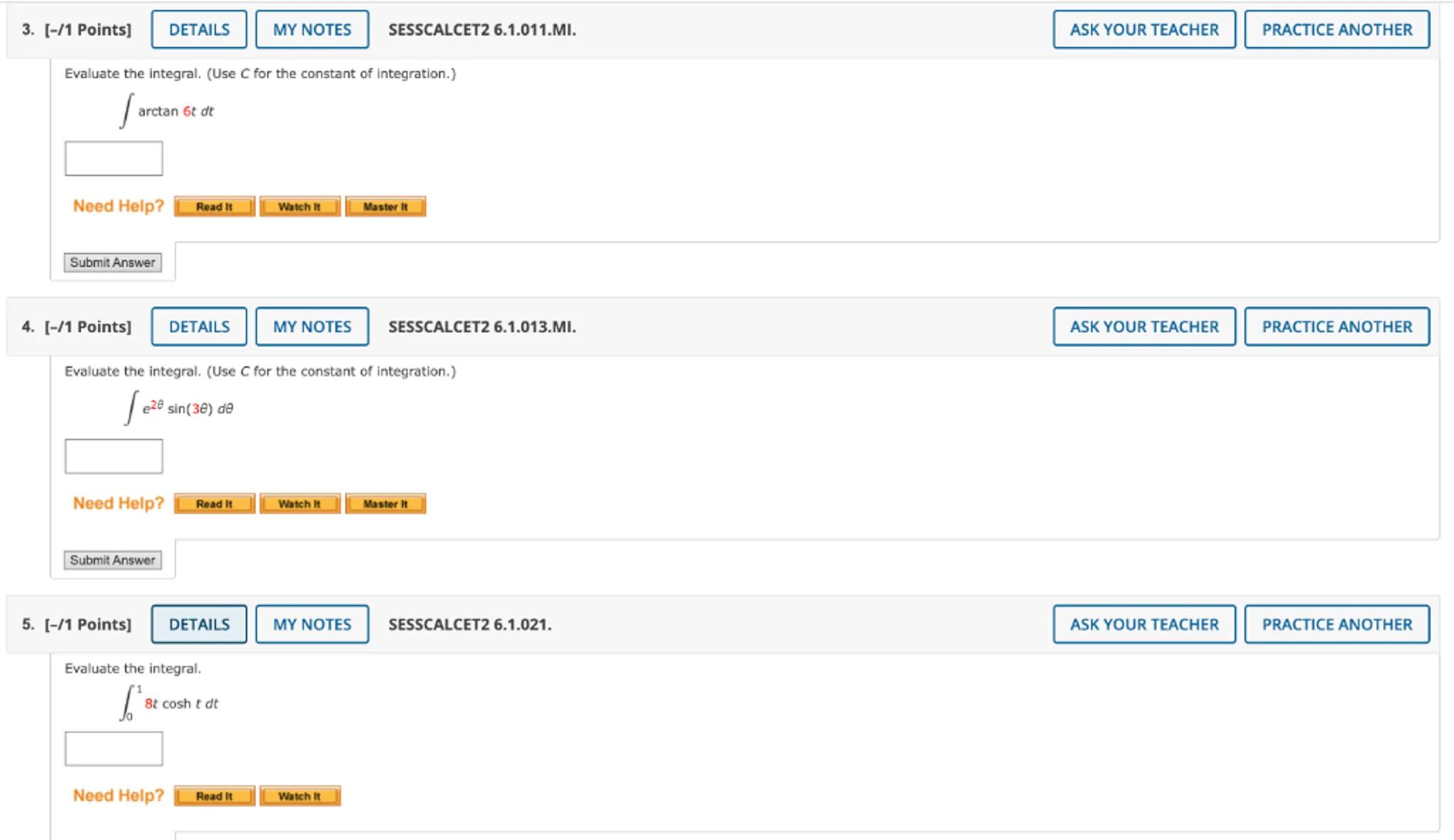

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Let
step 2
Use integration by parts: Let and
step 3
Compute and : and
step 4
Apply the integration by parts formula:
step 5
Substitute , , , and into the formula:
step 6
Simplify the integral:
step 7
Use substitution: Let , then
step 8
Rewrite the integral:
step 9
Integrate:
step 10
Combine results:
Answer
Key Concept
Integration by parts
Explanation
Integration by parts is used to integrate the product of two functions.
Question 2: Evaluate the integral
step 1
Let
step 2
Use integration by parts twice: Let and
step 3
Compute and : and
step 4
Apply the integration by parts formula:
step 5
Substitute , , , and into the formula:
step 6
Simplify the integral:
step 7
Use integration by parts again: Let and
step 8
Compute and : and
step 9
Apply the integration by parts formula:
step 10
Substitute , , , and into the formula:
step 11
Simplify the integral:
step 12
Combine results:
step 13
Solve for the integral:
step 14
Combine like terms:
step 15
Simplify:
step 16
Solve for :
step 17
Simplify:
Answer
Key Concept
Integration by parts
Explanation
Integration by parts is used to integrate the product of two functions, and sometimes it needs to be applied more than once.
Question 3: Evaluate the integral
step 1
Let
step 2
Use integration by parts: Let and
step 3
Compute and : and
step 4
Apply the integration by parts formula:
step 5
Substitute , , , and into the formula:
step 6
Evaluate the boundary term:
step 7
Simplify the integral:
step 8
Integrate:
step 9
Evaluate the boundary term:
step 10
Combine results:
Answer
Key Concept
Integration by parts
Explanation
Integration by parts is used to integrate the product of two functions, and boundary terms must be evaluated for definite integrals.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question