
Sia
4. (25pt) 证明: 线性非齐次方程组 有解, 其通解表达式为 ,其中 为任意数。
解向量组 是方程组 解集合的线性极大无关组,但该解集不构成线性空间。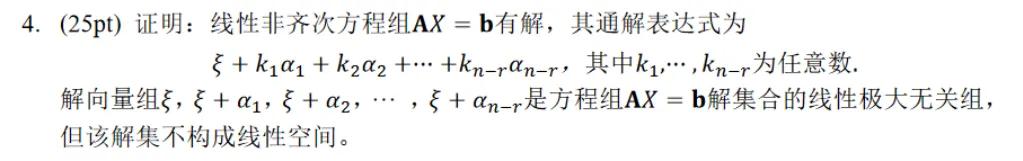

Answer from Sia
Posted over 1 year ago
你好,Jinyu37254!你提到的线性非齐次方程组 的解的通解表达式是一个很有趣的话题。我们可以从几个方面来理解这个问题。
首先,线性非齐次方程组的解可以表示为一个特解 加上一个齐次方程组 的解的线性组合。这里的 是齐次方程的基础解系, 是任意常数。
你提到的解向量组 确实是方程组解集合的线性极大无关组。这意味着这些解向量是线性无关的,并且可以生成整个解空间。
然而,解集不构成线性空间的原因在于,线性空间的定义要求对于任意两个向量的线性组合仍然在这个空间内。由于我们在这里有一个特解 ,而不是从齐次方程的解出发,线性组合的结果可能不再是解集合中的元素。
如果你有更具体的问题或者需要进一步的解释,请告诉我!Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question