
Sia
4 A motorway designer can assume that cars approaching a motorway enter a slip road with a velocity of and reach a velocity of before joining the motorway. Calculate the minimum length for the slip road, assuming that vehicles have an acceleration of .
[4]
5 A train is travelling at when the driver applies the brakes and gives the train a constant deceleration of magnitude for 100 s . Describe what happens to the train. Calculate the distance travelled by the train in 100 s.
6 A boy stands on a cliff edge and throws a stone vertically upwards at time
0 . The stone leaves his hand at . Take the acceleration of the ball as .
a Show that the equation for the displacement of the ball is:
[2]
[3]
b Calculate the height of the stone 2.0 s after release and 6.0 s after release.
[7]
c Calculate the time taken for the stone return to the level of the boy's hand. You may assume the boy's hand does not move vertically after the ball is released.
[4]
[Total: 9]
7 This graph shows the variation of velocity with time of two cars, A and B, which are travelling in the same direction over a period of time of 40 s .
Figure 2.35
Car A, travelling at a constant velocity of , overtakes car B at time 0 . In order to catch up with car A, car B immediately accelerates uniformly for 20 s to reach a constant velocity of . Calculate:
a the distance that A travels during the first 20 s
[2]
b the acceleration and distance of travel of B during the first 20 s
[5.
c the additional time taken for B to catch up with A
[2
d the distance each car will have then travelled since .
[2]
[Total: 11
8 An athlete competing in the long jump leaves the ground with a velocity of 5.6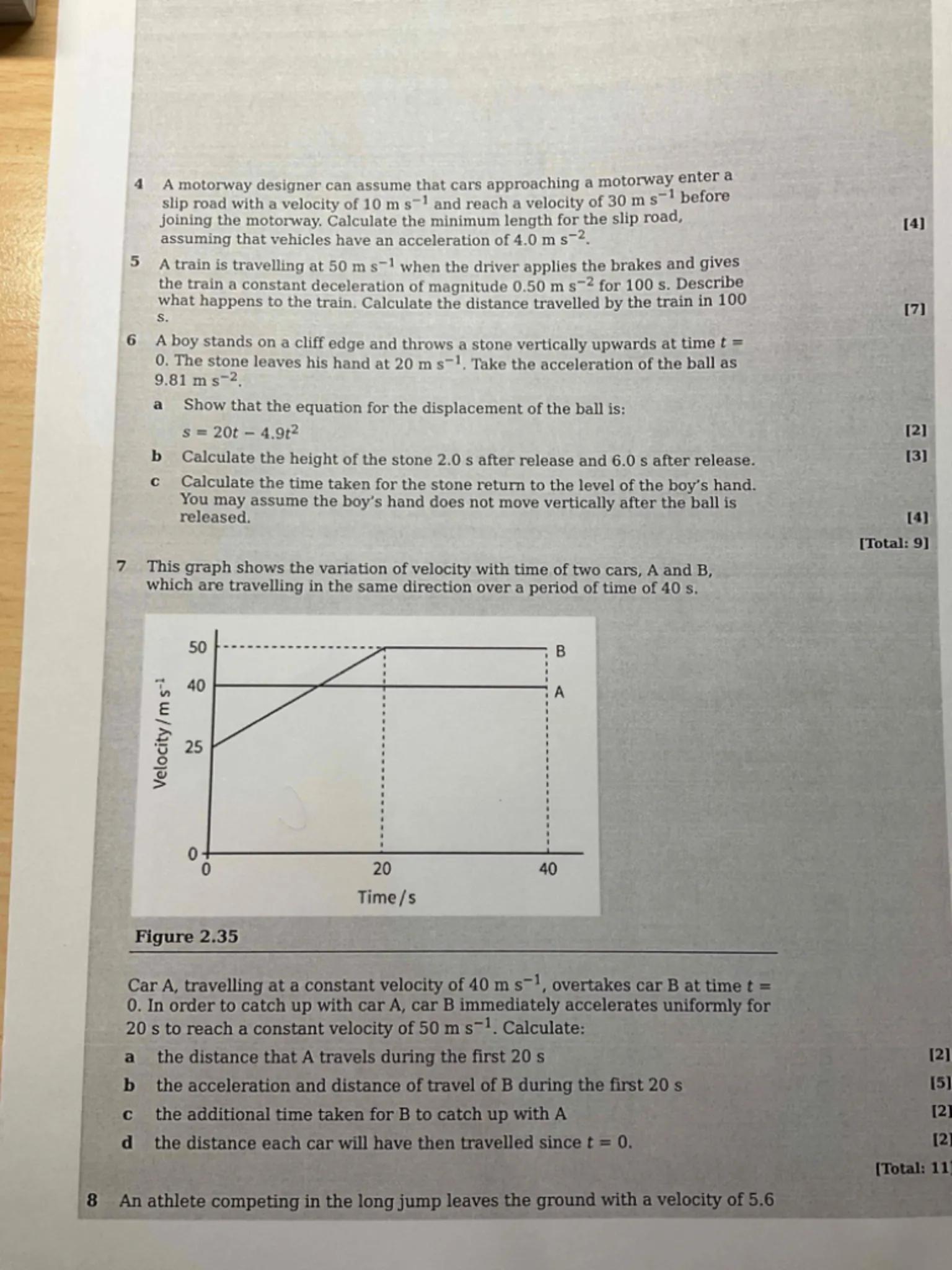

Answer from Sia
Posted about 1 year ago
Solution
a
To find the minimum length of the slip road, we can use the equation of motion for constant acceleration: . Here, the initial velocity , the final velocity , and the acceleration . First, we need to find the time it takes to accelerate from to using the formula . Rearranging gives us
b
Now, we can substitute the values into the distance equation: . Thus, the minimum length for the slip road is 100 meters
Answer
100 m
Key Concept
Kinematics and Equations of Motion: The equations of motion relate displacement, initial velocity, final velocity, acceleration, and time. The key equation used here is .
Explanation
The minimum length of the slip road is calculated by determining the time taken to accelerate and then using the distance formula for uniformly accelerated motion. This ensures that vehicles can safely reach the required speed before merging onto the motorway.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
