
Sia
4. The probable distance of an electron from the nucleus in atomic orbitals of Hydrogen and the -like ions are shown here for and of the atom, where distance from nucleus. These radial functions, , can be solved exactly for such systems. We assume that the wave functions are similar for the rest of the periodic table.
a) For total radial probability, we must include the small volume, or what we can call a voxel, as a function of distance from the nucleus to get a better idea of the location of the electron. Sketch the graph for in the box at the right.
distribution
b) Sketch the radial probability for each of the 3s, 3p and 3d orbitals on the axes provided below ( shown at right).
c) Considering the radial probability distribution functions for the and orbitals, and the ones that you have sketched in (b), explain the ordering of the energies of 3s, 3p, and 3d orbitals for all elements with more than one electron.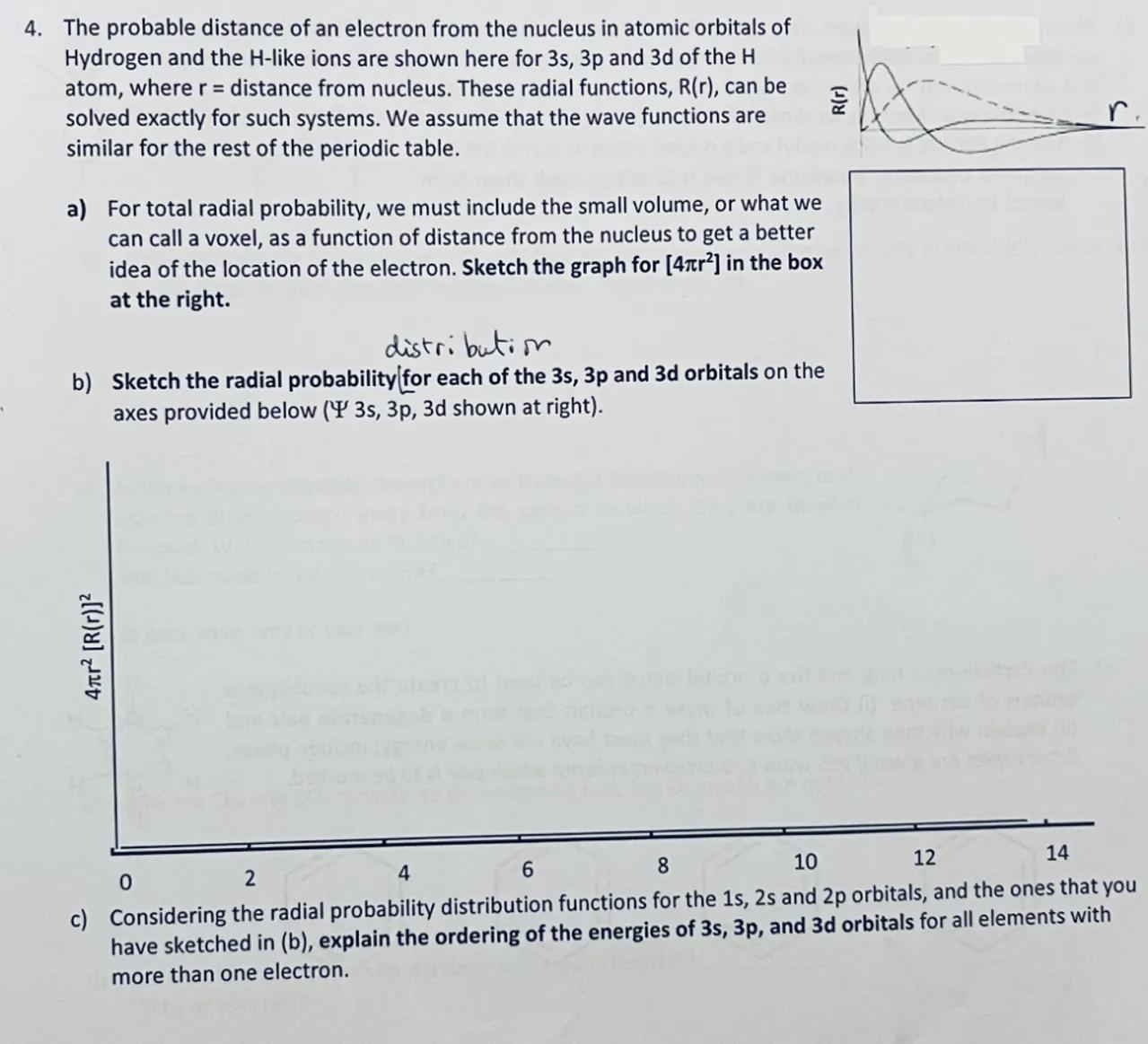

Answer from Sia
Posted over 1 year ago
Solution
1
Sketching the graph for \( 4\pi r^2 \): To sketch the graph of as a function of distance from the nucleus, we recognize that this is the formula for the surface area of a sphere with radius . As increases, the surface area increases quadratically
2
Sketching radial probability distributions: The radial probability distribution for an orbital is given by , where is the radial wave function. The shape of for 3s, 3p, and 3d orbitals can be inferred from the given small graph. The 3s orbital has one radial node, the 3p has two, and the 3d has three. The number of nodes increases with the angular momentum quantum number
3
Ordering of orbital energies: The energy of an orbital in multi-electron atoms is affected by both the principal quantum number and the angular momentum quantum number . For a given , orbitals with higher have higher energy due to less penetration of the electron cloud into the inner shells and increased electron-electron repulsion. Thus, for a given principal quantum number, the energy increases from s to p to d orbitals
1 Answer
The graph of will show a quadratic increase with increasing .
2 Answer
The radial probability distributions for 3s, 3p, and 3d orbitals will show increasing numbers of radial nodes as the angular momentum quantum number increases.
3 Answer
The energy ordering for orbitals within the same principal quantum number is 3s < 3p < 3d due to increasing angular momentum quantum number and electron-electron repulsion.
Key Concept
Radial probability distribution is the likelihood of finding an electron at a certain distance from the nucleus, and it is influenced by the shape of the radial wave function.
Explanation
The radial probability distribution graph for an orbital is obtained by multiplying the square of the radial wave function by the surface area of a sphere at a given radius , which is . The energy of orbitals increases with the angular momentum quantum number within a given principal quantum number due to electron shielding and repulsion effects.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question