
Sia
5. Consider the decomposition of the compound as follows:
When a 5.63-g sample of pure was sealed into an otherwise empty 2.50-L flask and heated to , the pressure in the flask gradually rose to and remained at that value. Calculate for this reaction.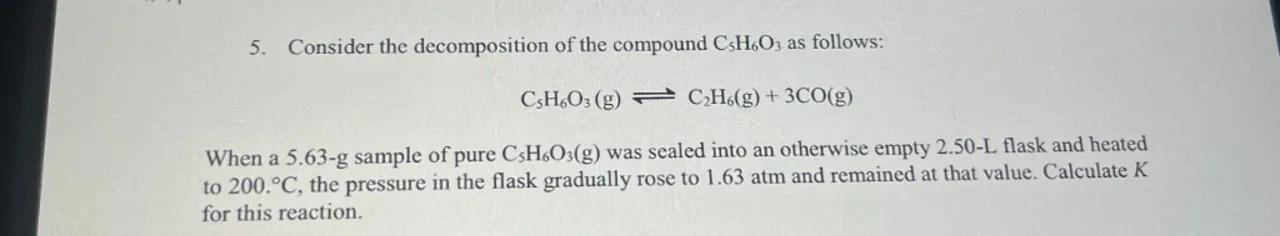

Answer from Sia
Posted over 1 year ago
Solution
1
Calculate moles of $\mathrm{C}_{5}\mathrm{H}_{6}\mathrm{O}_{3}$: First, we need to calculate the moles of that were initially present in the flask. The molar mass of is calculated by adding the atomic masses of its constituent atoms: . The number of moles is then found by dividing the mass of the sample by the molar mass:
2
Determine the change in moles: At equilibrium, let be the change in moles of that decomposed. This means moles of and moles of were formed
3
Write the expression for $K_p$: The equilibrium constant for the reaction in terms of partial pressures () is given by , where represents the partial pressure of each gas
4
Calculate partial pressures using the ideal gas law: Since the total pressure at equilibrium is 1.63 atm and the volume of the flask is 2.50 L, we can use the ideal gas law () to find the total moles of gas at equilibrium. We assume the temperature () is constant at 200 °C, which is 473.15 K in Kelvin. The ideal gas constant () is 0.0821 L·atm/(mol·K)
5
Establish the equilibrium mole fractions: The mole fraction of each gas can be used to find its partial pressure. If is the total number of moles at equilibrium, then the partial pressure of each gas is
6
Solve for $x$ and calculate $K_p$: Using the relationships established in steps 2 and 5, we can set up equations to solve for and then use the values of to calculate the partial pressures and subsequently
Answer
[Insert final answer here]
Key Concept
The equilibrium constant is calculated using the partial pressures of the reactants and products at equilibrium.
Explanation
To find , we need to determine the moles of reactants and products at equilibrium, convert those to partial pressures, and then apply the equilibrium expression.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question