
Sia
7:53
5G
88
wooclap
Got it!
Confused
Given defined for , what is the nature of ?
Converging
Diverging
Submit
app.wooclap.com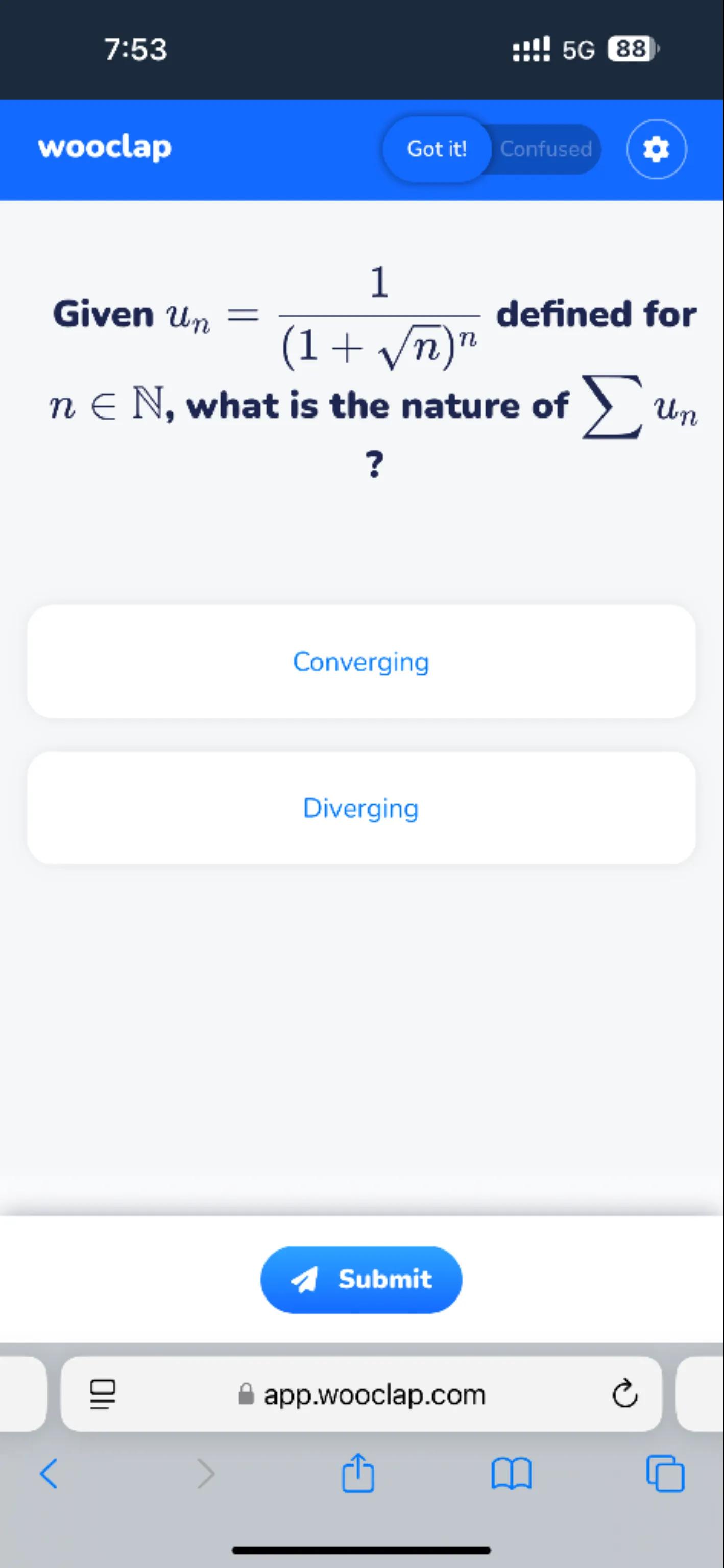

Answer from Sia
Posted about 1 year ago
Solution by Steps
step 2
We can rewrite as . Taking the limit, we have
step 3
As approaches infinity, dominates, and we can approximate as . Thus,
step 4
Since approaches 0, we can apply the ratio test or comparison test to determine the nature of the series. The terms decrease rapidly, indicating convergence
step 5
Therefore, the series converges
A
Key Concept
Convergence of Series
Explanation
A series converges if the terms approach zero and decrease sufficiently fast, which is the case for .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question