
Sia

Question
Math
Posted over 1 year ago
A pharmaceutical scientist making a new medication wonders how much of the active ingredient to include in a dose. They are curious how long different amounts of the active ingredient will stay in someone's bloodstream.
The amount of time (in hours) the active ingredient remains in the bloodstream can be modeled by , where is the initial amount of the active ingredient (in milligrams). Here is the graph of and the graph of the line .
Which statements represent the meaning of the intersection point of the graphs?
Choose all answers that apply:
A It describes the amount of time the active ingredient stays in the bloodstream if the initial amount of the active ingredient is .
B It gives the solution to the equation .
c. It describes the situation where the initial amount of the active ingredient is equal to how long it stays in the bloodstream.
D It gives the initial amount of the active ingredient such that the last of the active ingredient leaves the bloodstream after 4 hours.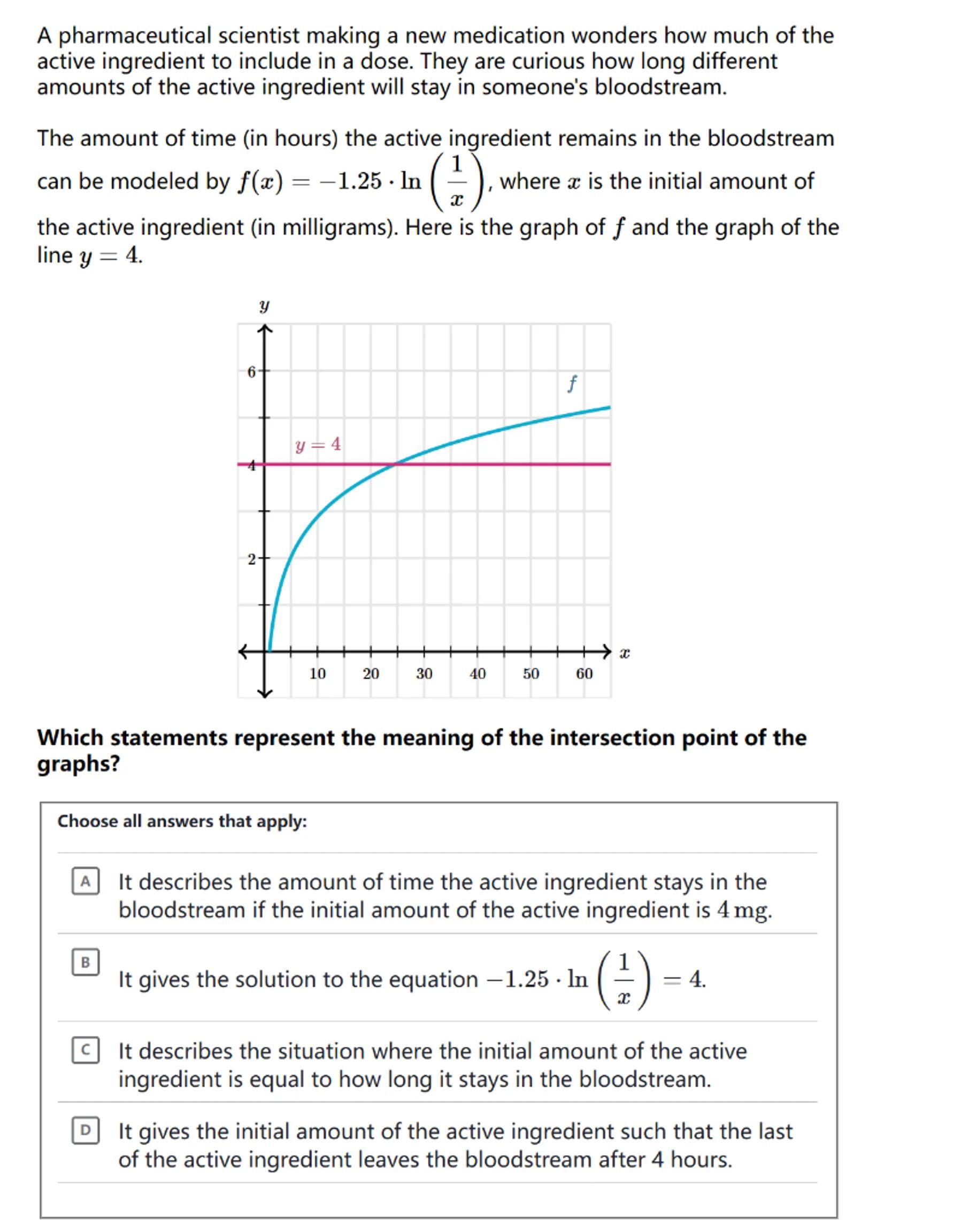

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
The intersection point occurs where . Therefore, at the intersection,
step 3
To solve for , we can use the property of logarithms that implies
step 4
Applying this property to our equation, we get , which simplifies to
step 5
The value of represents the initial amount of the active ingredient in milligrams such that the active ingredient stays in the bloodstream for 4 hours
[question number] Answer
B
Key Concept
Intersection Point of Graphs
Explanation
The intersection point of the graph of a function and a horizontal line represents the solution to the equation formed by setting the function equal to the y-value of the horizontal line.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question