
Sia

Question
Math
Posted over 1 year ago
A scientist studying water quality measures the lead level in parts per billion (ppb) at each of 49 randomly chosen locations along a water line. Suppose that the lead levels across all the locations on this line are strongly skewed to the right with a mean of and a standard deviation of . Assume that the measurements in the sample are independent.
What is the probability that the mean lead level from the sample of 49 measurements is less than ?
Choose 1 answer:
(A)
(B)
(C)
(D)
(E) We cannot calculate this probability because the sampling distribution is not normal.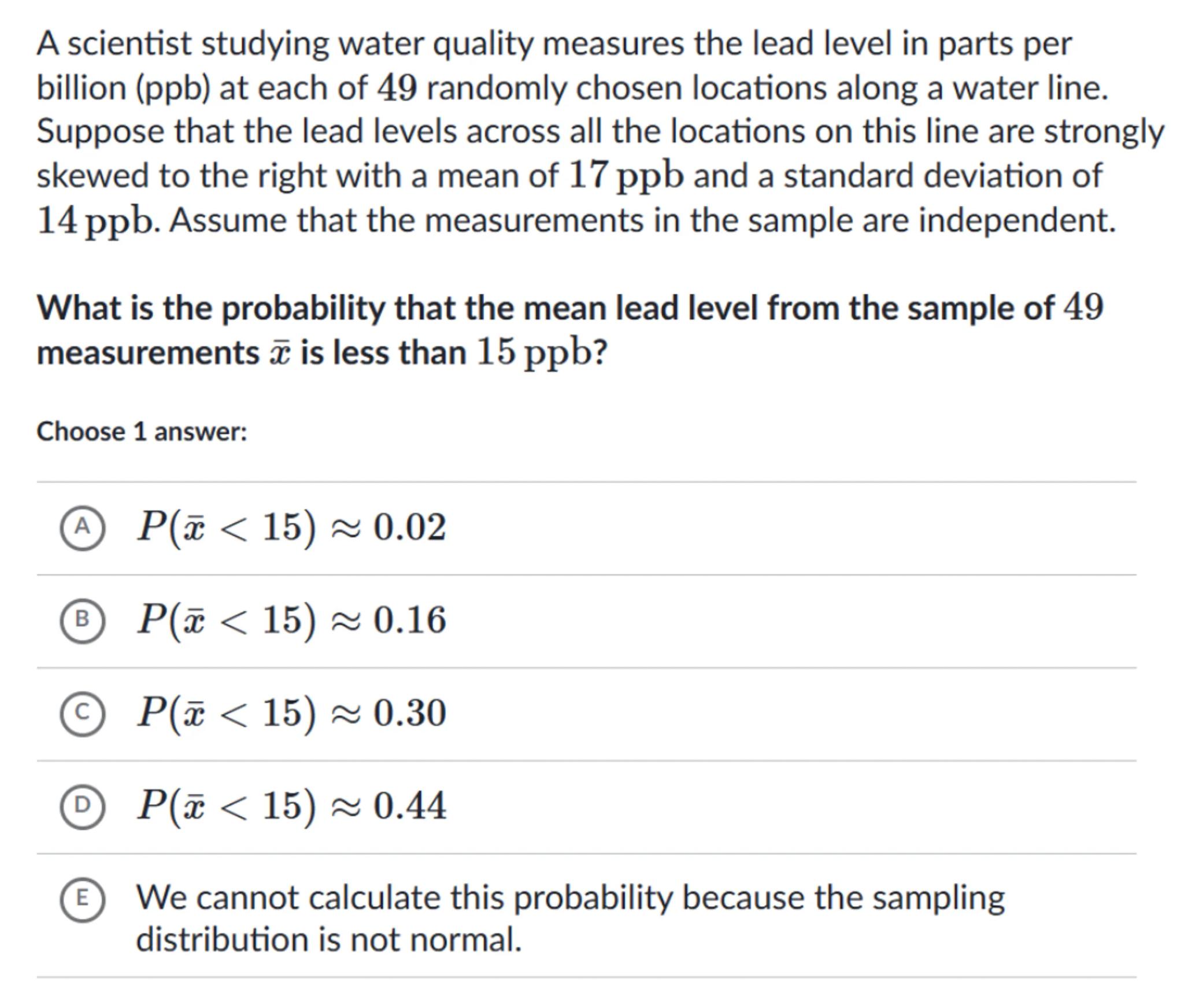

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
We calculate the Z-score for using the formula , where ppb is the population mean, ppb is the population standard deviation, and is the sample size
step 3
Substituting the values into the Z-score formula gives
step 4
We look up the Z-score of -1 in the standard normal distribution table or use a calculator to find the cumulative probability
step 5
The cumulative probability for Z = -1 is approximately 0.16. This is the probability that the sample mean is less than 15 ppb
B
Key Concept
Central Limit Theorem
Explanation
The Central Limit Theorem states that the sampling distribution of the sample mean will be approximately normally distributed, regardless of the population distribution, provided the sample size is sufficiently large. In this case, with a sample size of 49, we can assume the sampling distribution of the mean is approximately normal even though the population distribution is skewed.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question