
Sia

Question
Math
Posted over 1 year ago
A sociologist studying fertility in France and Switzerland wanted to test if there was a difference in the average number of babies women in each country have. The sociologist obtained a random sample of women from each country. Here are the results of their test:
\begin{tabular}{lrrrr}
& \multicolumn{2}{c}{ \# of babies } & & \\
Country & & Mean & StDev & SE mean \\
\hline France & 100 & 1.85 & 1.3 & 0.13 \\
Switzerland & 100 & 1.65 & 1.2 & 0.12 \\
test for & & & &
\end{tabular}
Assume that all conditions for inference have been met.
At the level of significance, is there sufficient evidence to conclude that there is a difference in the average number of babies women in each country have?
Choose 1 answer:
(A) Yes, since the -value is greater than 0.05 .
(B) Yes, since the test statistic is greater than 0.05 .
(C) No, since the -value is greater than 0.05 .
(D) No, since the test statistic is greater than 0.05 .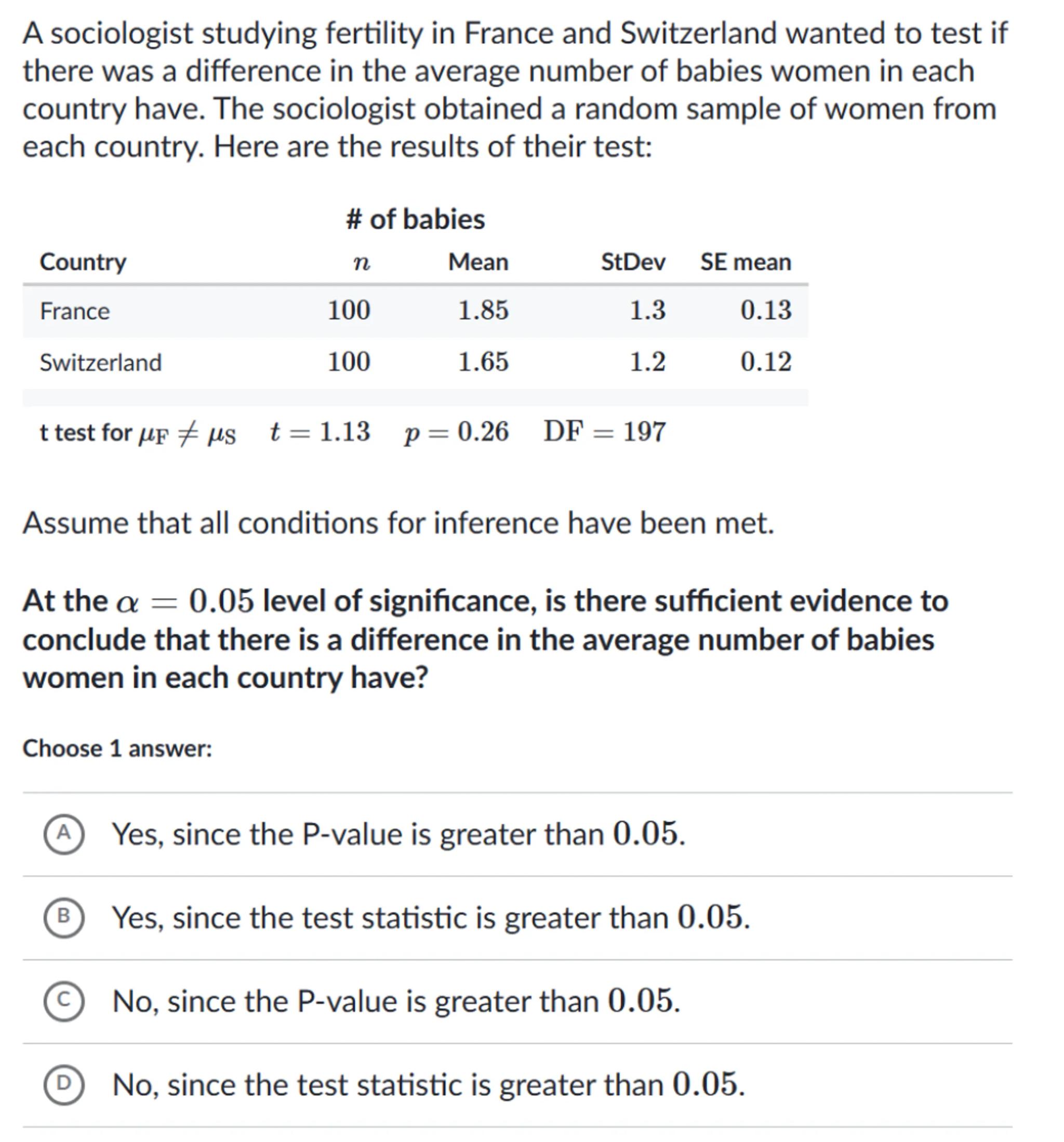

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
Compare the p-value to the significance level
step 3
Make a decision based on the comparison. If the p-value is less than or equal to the significance level, reject the null hypothesis. If the p-value is greater than the significance level, fail to reject the null hypothesis
step 4
Apply this decision rule to the given p-value of 0.26 and the significance level of 0.05
step 5
Since the p-value (0.26) is greater than the significance level (0.05), we fail to reject the null hypothesis
C
Key Concept
Hypothesis Testing and P-value
Explanation
In hypothesis testing, if the p-value is greater than the significance level (α), there is not enough evidence to reject the null hypothesis.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question