
Sia

Question
Math
Posted over 1 year ago
A website offers a coupon such that each customer has a chance of getting the coupon each day they visit the site. Aya visits the website for 6 consecutive days.
What is the probability that Aya will be offered a coupon on at least one of the days she visits the website?
Round your answer to the nearest hundredth.
at least one coupon 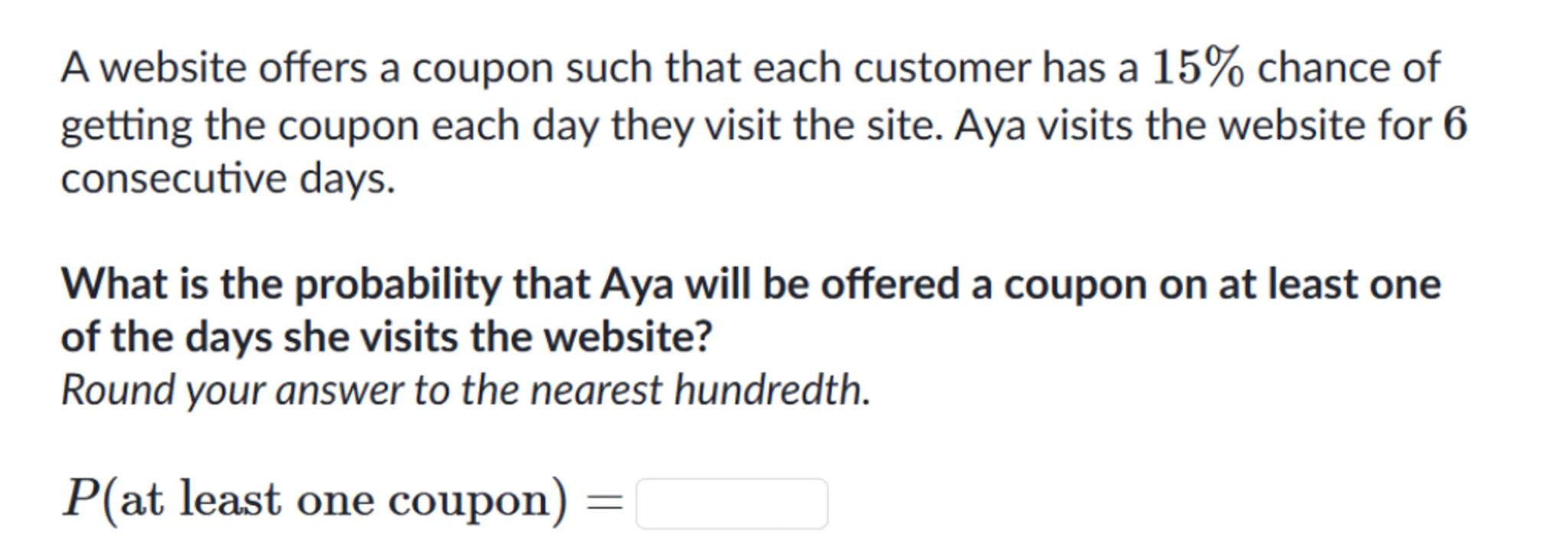

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Calculate the probability that Aya does not get a coupon on a single day, which is
step 2
Calculate the probability that Aya does not get a coupon on any of the 6 days she visits, which is
step 3
Use the asksia-ll calculator result for , which is
step 4
Subtract this probability from 1 to find the probability that Aya gets a coupon on at least one day, which is
step 5
Calculate the final probability, which is
step 6
Round the final probability to the nearest hundredth, which is
[1] Answer
at least one coupon
Key Concept
Complementary Probability
Explanation
The probability of Aya receiving at least one coupon is found by subtracting the probability of her not receiving a coupon on any day from 1. This is known as the complementary probability.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question