
Sia

Question
Macroeconomics
Posted over 1 year ago
Alex and Henry are completing group work for class. The input table below gives the time that it takes Henry and Alex to complete their homework assignments in hours.
\begin{tabular}{lll}
& Time to complete Worksheets & Time to complete Essays \\
\hline Henry & 1 hour & 2 hours \\
Alex & 1 hour & 3 hours
\end{tabular}
Assuming Alex and Henry decide to specialize and trade essays and worksheets with one another, what would be a terms of trade or exchange price that would satisfy both of them?
Choose 1 answer:
(A) Any price where an essay costs less than 2 worksheets
(B) Any price where an essay costs between 2 and 3 worksheets
(c) Any price where an essay costs more than 3 worksheets
(D) We cannot determine a mutually agreeable trading price
(E) Any trading price is possible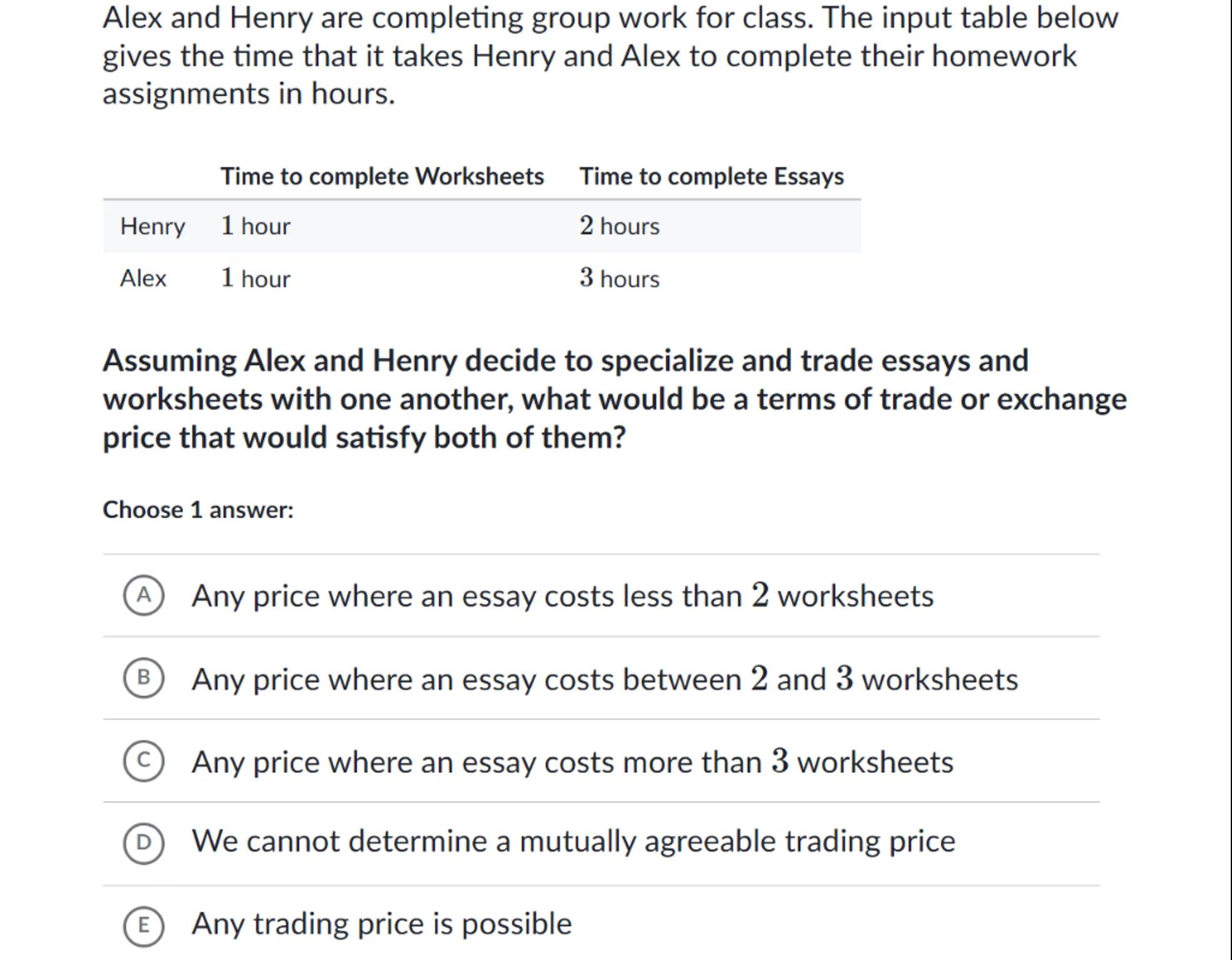

Answer from Sia
Posted over 1 year ago
Solution
a
Comparative Advantage: Comparative advantage occurs when a person can produce a good at a lower opportunity cost than another person
b
Henry's Opportunity Cost: Henry takes 1 hour to complete a worksheet and 2 hours to complete an essay. Therefore, the opportunity cost of 1 essay for Henry is 2 worksheets
c
Alex's Opportunity Cost: Alex takes 1 hour to complete a worksheet and 3 hours to complete an essay. Therefore, the opportunity cost of 1 essay for Alex is 3 worksheets
d
Terms of Trade: For both to benefit from trade, the terms of trade must lie between their opportunity costs. Hence, the price of 1 essay should be between 2 and 3 worksheets
Answer
(B) Any price where an essay costs between 2 and 3 worksheets
Key Concept
Comparative Advantage
Explanation
Comparative advantage is the ability to produce a good at a lower opportunity cost. In this scenario, Henry and Alex should trade at a price where the opportunity cost of producing an essay is between 2 and 3 worksheets, benefiting both parties.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question