
Sia

Question
Math
Posted over 1 year ago
Angle is circumscribed about circle .
What is the measure of ?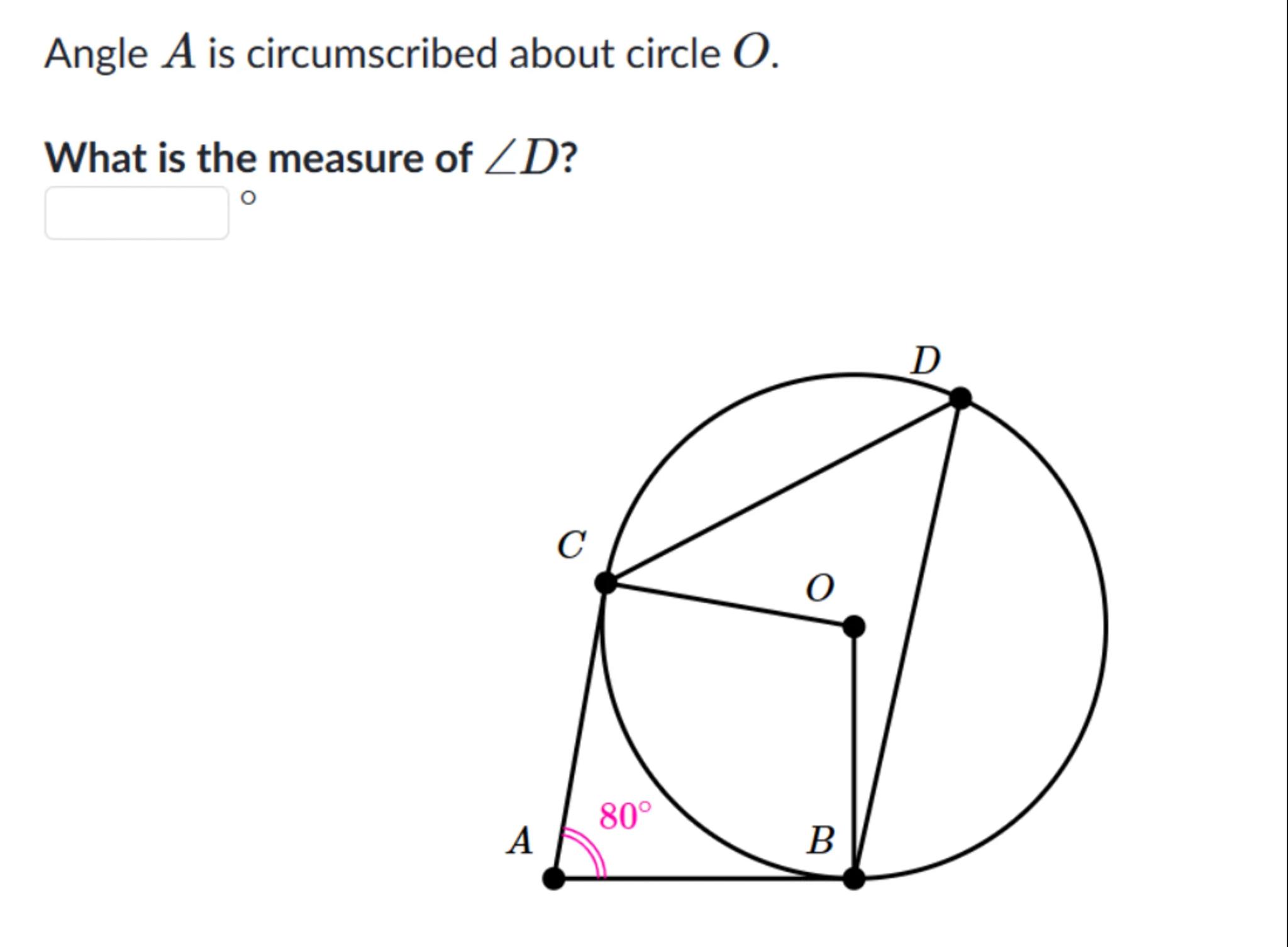

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Identify the relationship between the inscribed angle and the central angle that subtends the same arc
step 2
Recognize that angle is an inscribed angle that subtends arc
step 3
Understand that the central angle that subtends arc is twice the inscribed angle
step 4
Calculate the measure of the central angle using the given measure of angle :
step 5
Note that angle is also a central angle that subtends arc
step 6
Realize that the sum of the central angles and that subtend the entire circle must be
step 7
Calculate the measure of angle :
Answer
The measure of is .
Key Concept
Inscribed Angle and Central Angle
Explanation
The inscribed angle is half the measure of the central angle that subtends the same arc. The sum of all central angles in a circle is .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question