
Sia
Assessment
Support
?
:三 Completed 22 of 22 Questions
FAQ
Grading Settings
Show
Question 2 of 22
Srest Quarion
Q1
Ungraded
Q2
points
Q3
points
Q4
(a)
Devely
,
C
64
2x points
Q5
points
Q6
(b)
0
2x points
(c) 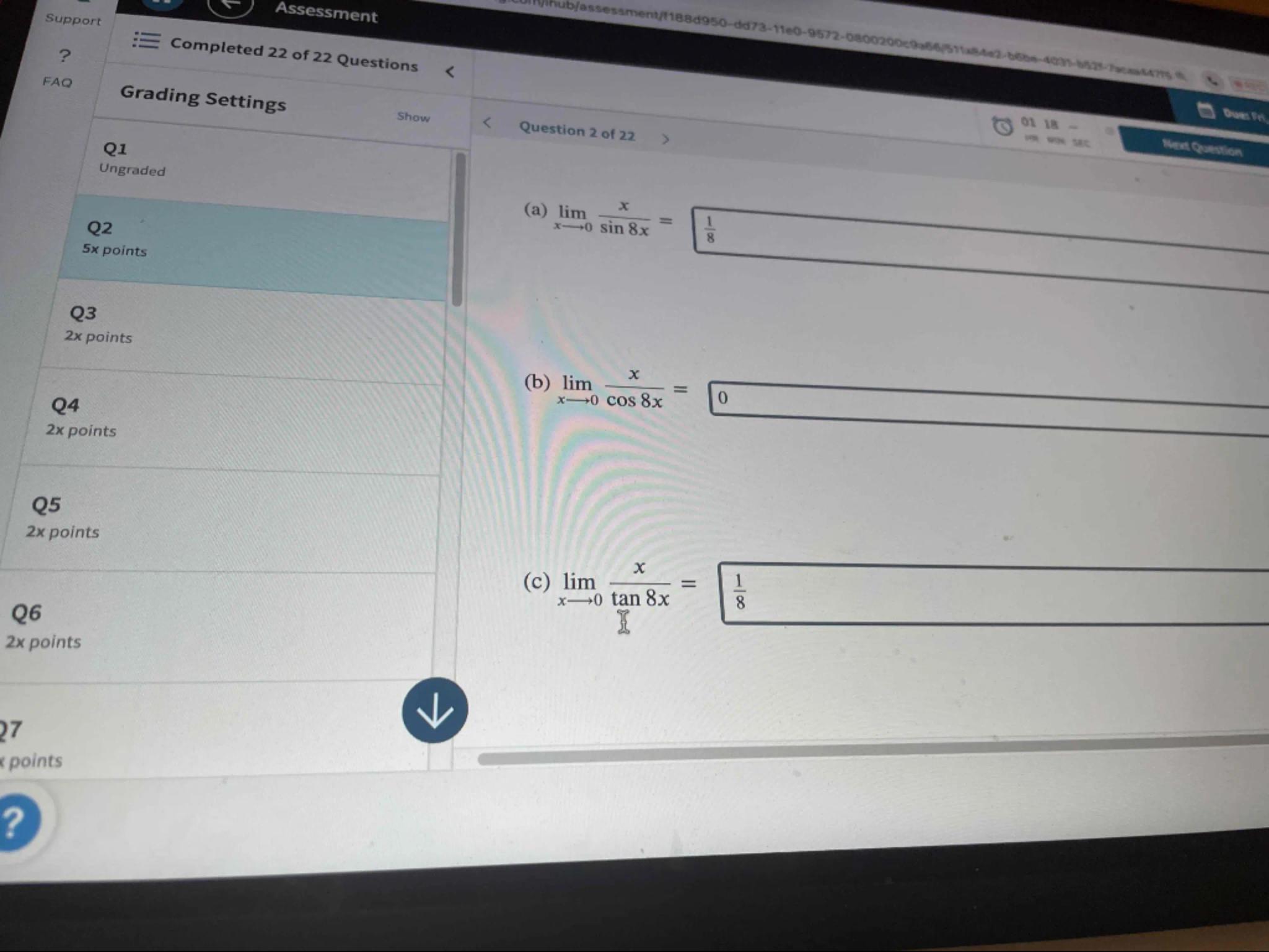

Answer from Sia
Posted about 1 year ago
Solution by Steps
step 1
To find the derivative of the function , we apply the quotient rule, which states that if , then . Here, and
step 2
The derivatives are (since is a constant) and
step 3
Substituting into the quotient rule gives
Answer
Key Concept
Quotient Rule for Derivatives
Explanation
The quotient rule is used to differentiate functions that are the ratio of two other functions, allowing us to find the derivative accurately.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
