
Sia
Consider the following matrix , and let . Find , and . (i.e., find the entries in the third row of ).
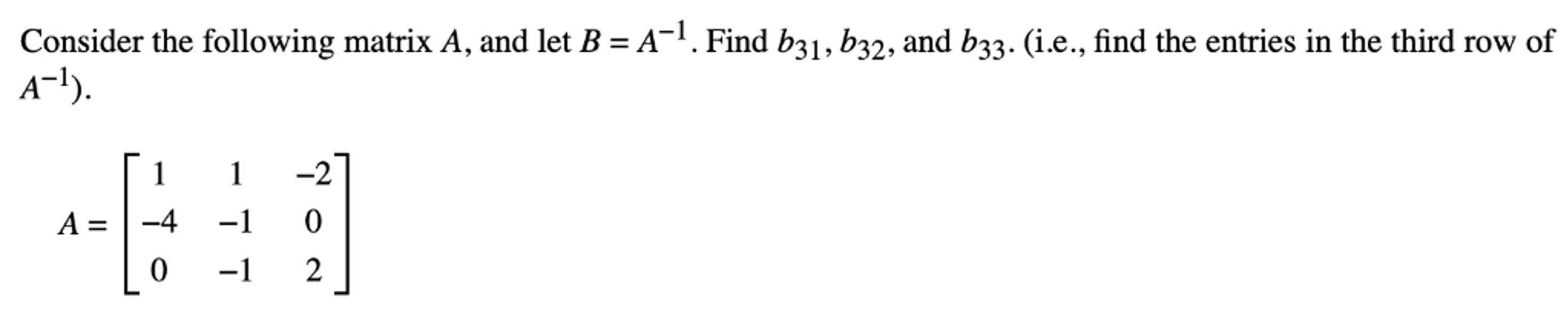

Answer from Sia
Posted almost 2 years ago
Solution by Steps
step 1
To find the inverse of matrix , we first need to write down the matrix :
step 2
Calculate the determinant of matrix . The determinant of a 3x3 matrix is given by:
For our matrix :
step 3
Find the matrix of minors for . The minor of an element is the determinant of the 2x2 matrix that remains after removing the row and column of that element:
step 4
Find the matrix of cofactors by applying the checkerboard pattern of signs to the matrix of minors:
step 5
Transpose the matrix of cofactors to get the adjugate matrix:
step 6
Finally, divide the adjugate matrix by the determinant to get the inverse of :
step 7
The entries in the third row of are:
Answer
The entries in the third row of are , , and .
Key Concept
Matrix Inversion
Explanation
To find the inverse of a 3x3 matrix, we use the determinant and the adjugate matrix. The inverse is given by the adjugate matrix divided by the determinant.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question