
Sia

Question
Math
Posted over 1 year ago
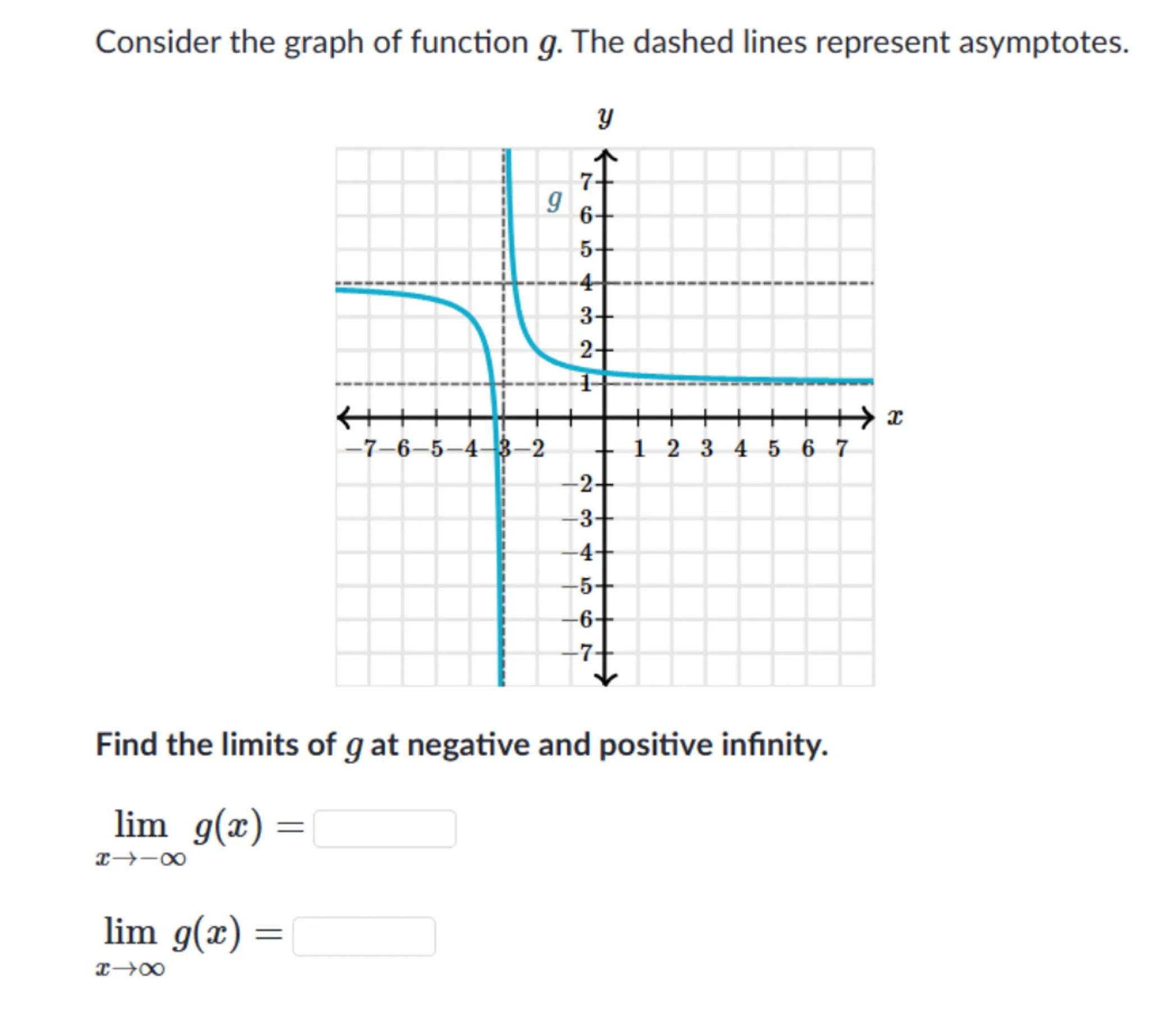
Consider the graph of function . The dashed lines represent asymptotes.
Find the limits of at negative and positive infinity.

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find the limit of as approaches negative infinity, we observe the behavior of the graph on the left side. The graph of starts horizontally at approximately and then approaches negative infinity as it nears the dashed line at . Therefore,
step 2
To find the limit of as approaches positive infinity, we observe the behavior of the graph on the right side. The graph of comes from positive infinity along the dashed line at and then becomes mostly horizontal near . Therefore,
Answer
and
Key Concept
Limits at infinity
Explanation
The limits at infinity describe the behavior of the function as approaches very large positive or negative values. In this case, the graph shows horizontal asymptotes indicating the function's values as goes to negative and positive infinity.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question