
Sia

Question
Math
Posted over 1 year ago
Esteban suspects that right-handed participants have an unfair advantage on a memory test because the input device uses the right hand. He selects a random sample of existing test data and summarizes it in the following table.
\begin{tabular}{lll}
\multicolumn{3}{c}{ Scores on memory test (points) } \\
& Left-handed & Right-handed \\
\hline Sample mean & & \\
Sample standard deviation & & \\
Sample size & &
\end{tabular}
Assume that the conditions for inference have been met.
Let be the difference in mean score of the right- and left-handed participants.
Which of the following is a confidence interval for ?
Use a calculator with statistical capabilities to calculate the interval.
Choose 1 answer:
(A)
(B)
(C)
(D) 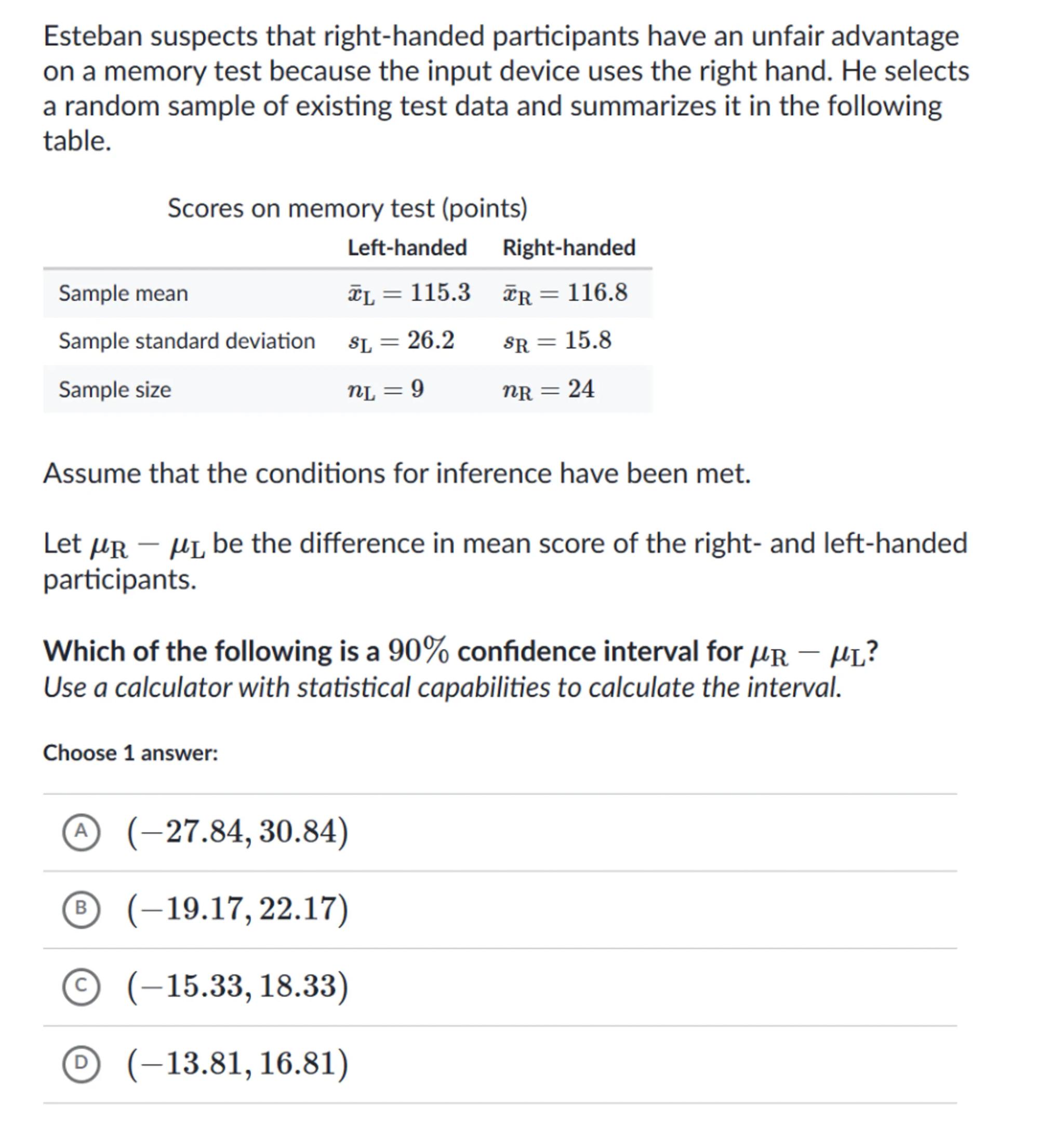

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
Substitute the given values into the formula:
step 3
Calculate the value of SE:
step 4
Determine the z-score for a 90% confidence interval, which is approximately 1.645 for a two-tailed test
step 5
Calculate the margin of error (ME) using the formula
step 6
Substitute the values into the formula:
step 7
Calculate the confidence interval using the formula
step 8
Substitute the values into the formula:
step 9
Calculate the lower and upper bounds of the confidence interval: Lower bound , Upper bound
step 10
Round the values to two decimal places if necessary: CI
D
Key Concept
Confidence Interval for the Difference in Means
Explanation
The confidence interval for the difference between two means is calculated using the standard error of the difference, the appropriate z-score for the confidence level, and the sample means. The margin of error is then applied to the difference in sample means to find the interval.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question