
Sia
Evaluate the currents, voltage across resistors, power absorbed
Check KCL and KCL
Practice Problem 1
Figure m2.3 Circuit for Problem m2.3.
Consider
Find and V3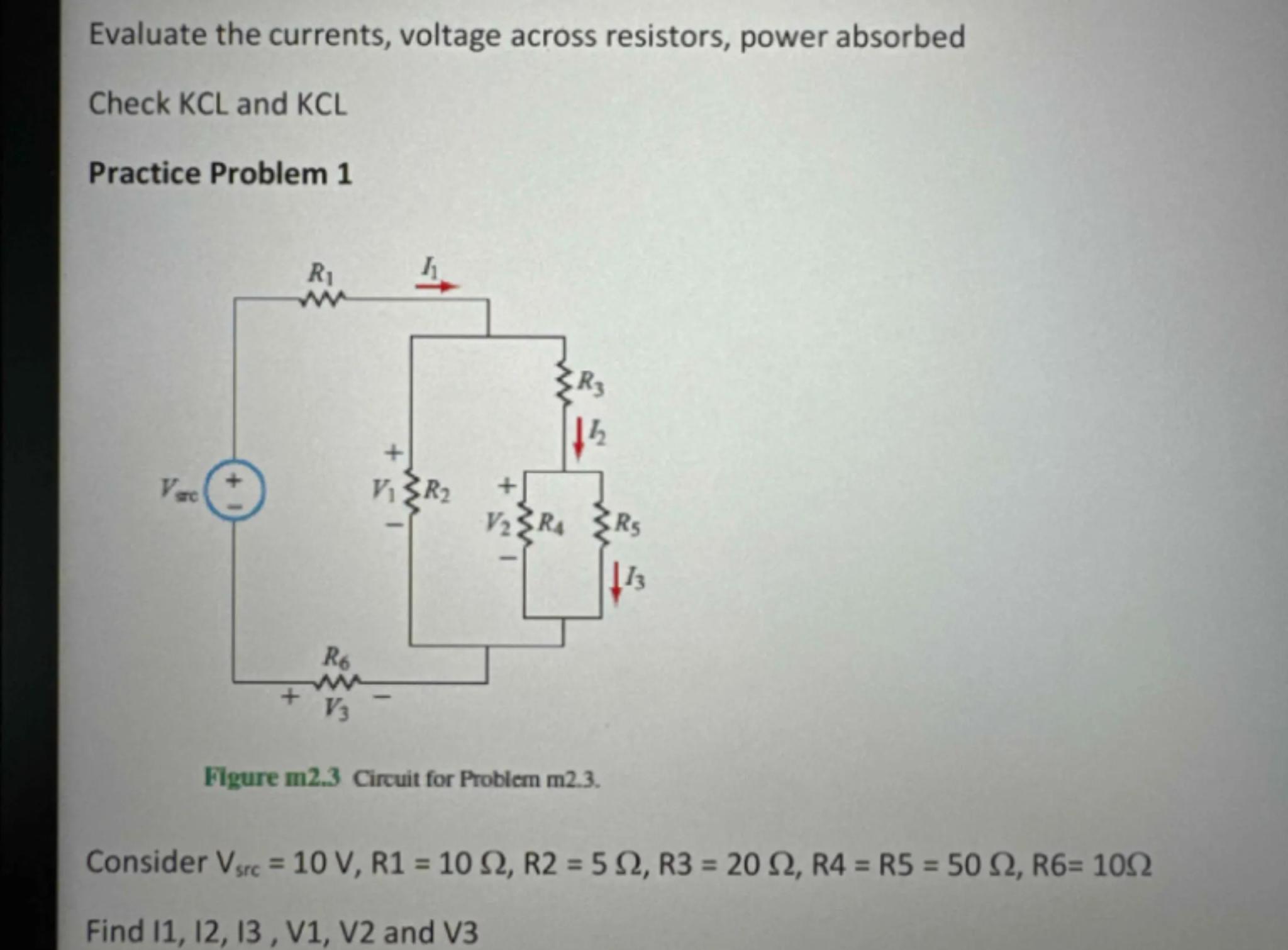

Answer from Sia
Posted about 1 year ago
Answer
Solution
a
Apply Kirchhoff's Voltage Law (KVL) to the loop containing , , and :
Substituting the values, we have:
This simplifies to:
b
Use Ohm's Law to find and :
c
Apply KCL at the node where , , and connect:
The current entering the node is and the currents leaving are and :
Using Ohm's Law for , , and :
Thus,
However, since also flows through , we need to recalculate as:
So,
d
Calculate across :
Using KVL again, we find:
However, since is in series with , we can find the voltage across as:
Key Concept
Application of KVL and KCL in circuit analysis
Explanation
The solution involves applying Kirchhoff's laws to find the currents and voltages in the circuit systematically.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question