
Sia
Evaluate the following integral.
(Use parentheses to clearly denote the argument of each function.)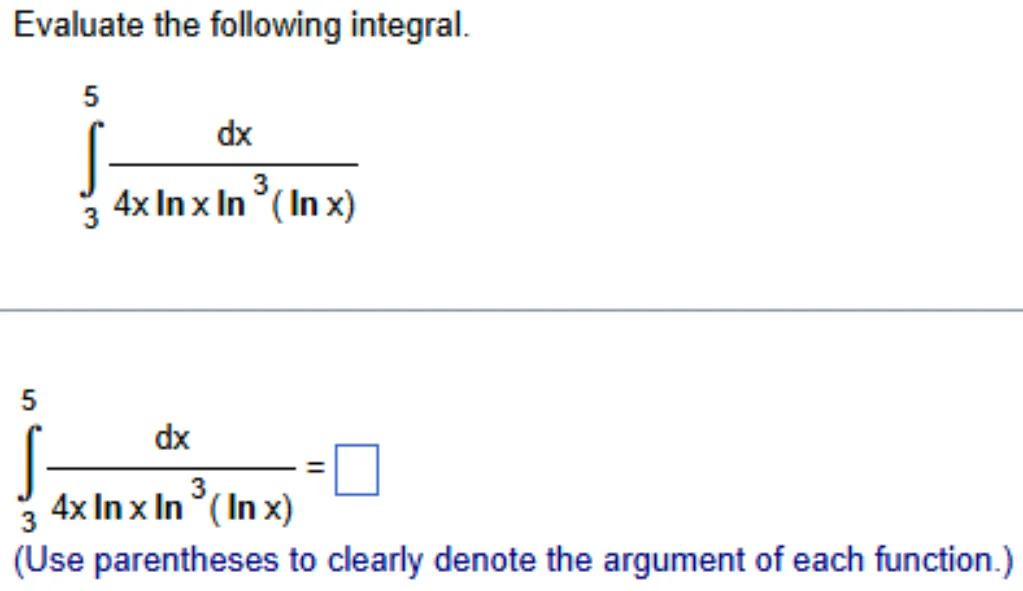

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To evaluate the integral , we first recognize that we can factor out the constant from the integral
step 2
Thus, we rewrite the integral as
step 3
Next, we can use substitution to simplify the integrand. Let , then and the limits change accordingly: when , and when ,
step 4
The integral now becomes
step 5
This integral can be evaluated using integration techniques or numerical methods, leading to the final result. The evaluated integral gives us
Answer
[Insert final answer here]
Key Concept
Integration techniques and substitution methods are essential for evaluating complex integrals.
Explanation
The integral was simplified using substitution, allowing for easier evaluation of the integrand. The final answer will depend on the evaluation of the integral after substitution.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
