
Sia

Question
Math
Posted over 1 year ago
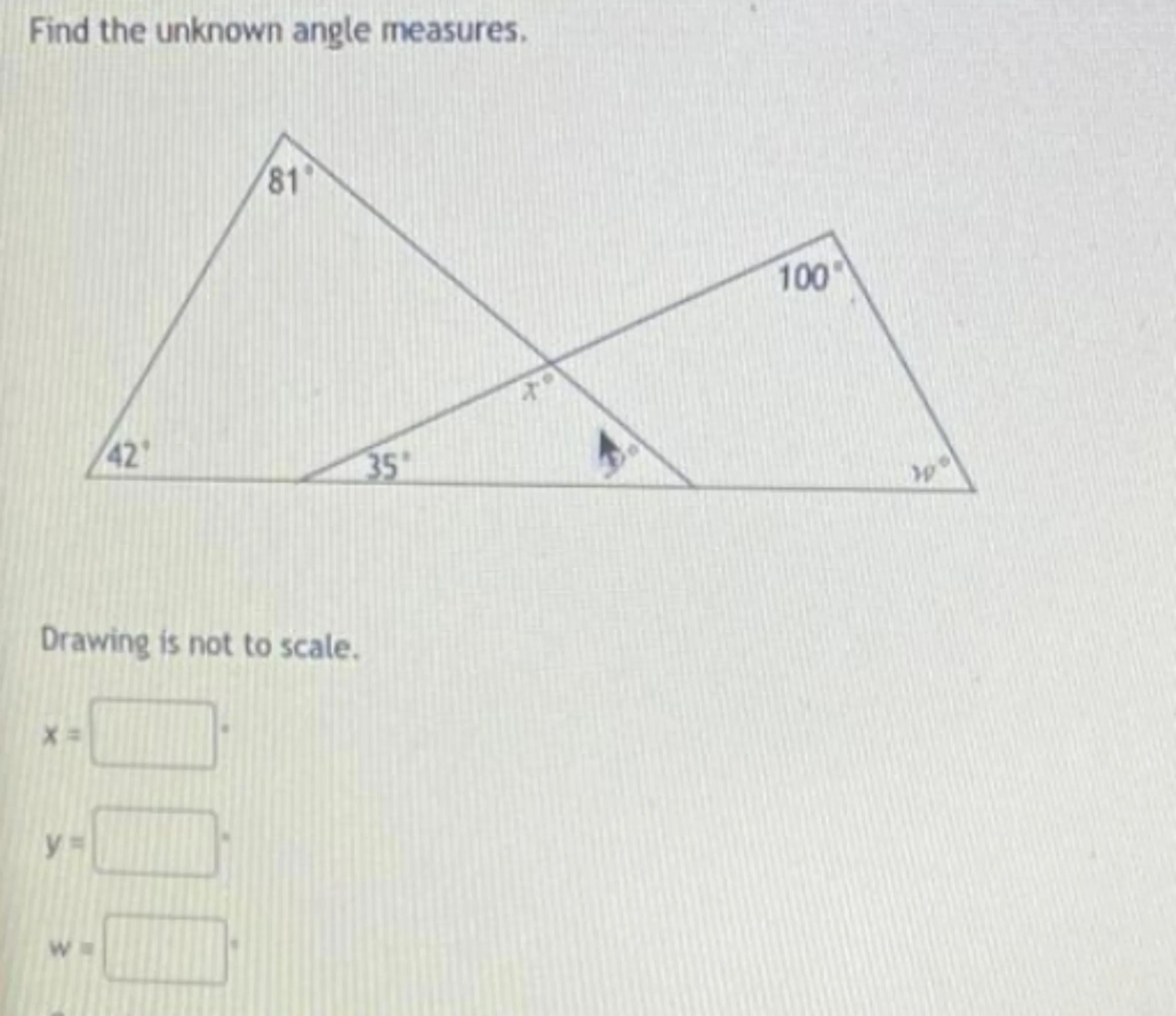
Find the unknown angle measures.
Drawing is not to scale.

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Identify the known angles in the left triangle. The angles are 81 degrees and 42 degrees
step 2
Use the fact that the sum of angles in a triangle is 180 degrees to find the unknown angle in the left triangle
step 3
Calculate the unknown angle: . Therefore, the unknown angle in the left triangle is 57 degrees
step 4
Identify the known angles in the right triangle. The angles are 100 degrees and y degrees
step 5
Use the fact that the sum of angles in a triangle is 180 degrees to find the unknown angle in the right triangle
step 6
Calculate the unknown angle: . Therefore, the unknown angle in the right triangle is
step 7
Since the two triangles share a common angle labeled as x degrees, we know that
step 8
The angle w is formed by the intersection of the two triangles. Since the sum of angles around a point is 360 degrees, we can find w by subtracting the known angles from 360 degrees
step 9
Calculate w: . Therefore,
step 10
The angle y can be found by using the fact that the sum of angles in the right triangle is 180 degrees. Since we already know that , we can use this to find y
step 11
Calculate y: . Therefore,
Answer
, ,
Key Concept
Sum of angles in a triangle
Explanation
The sum of the angles in any triangle is always 180 degrees. This property allows us to find unknown angles when the other angles are known.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question