
Sia

Question
Math
Posted over 1 year ago
Find the value of in the triangle shown below.
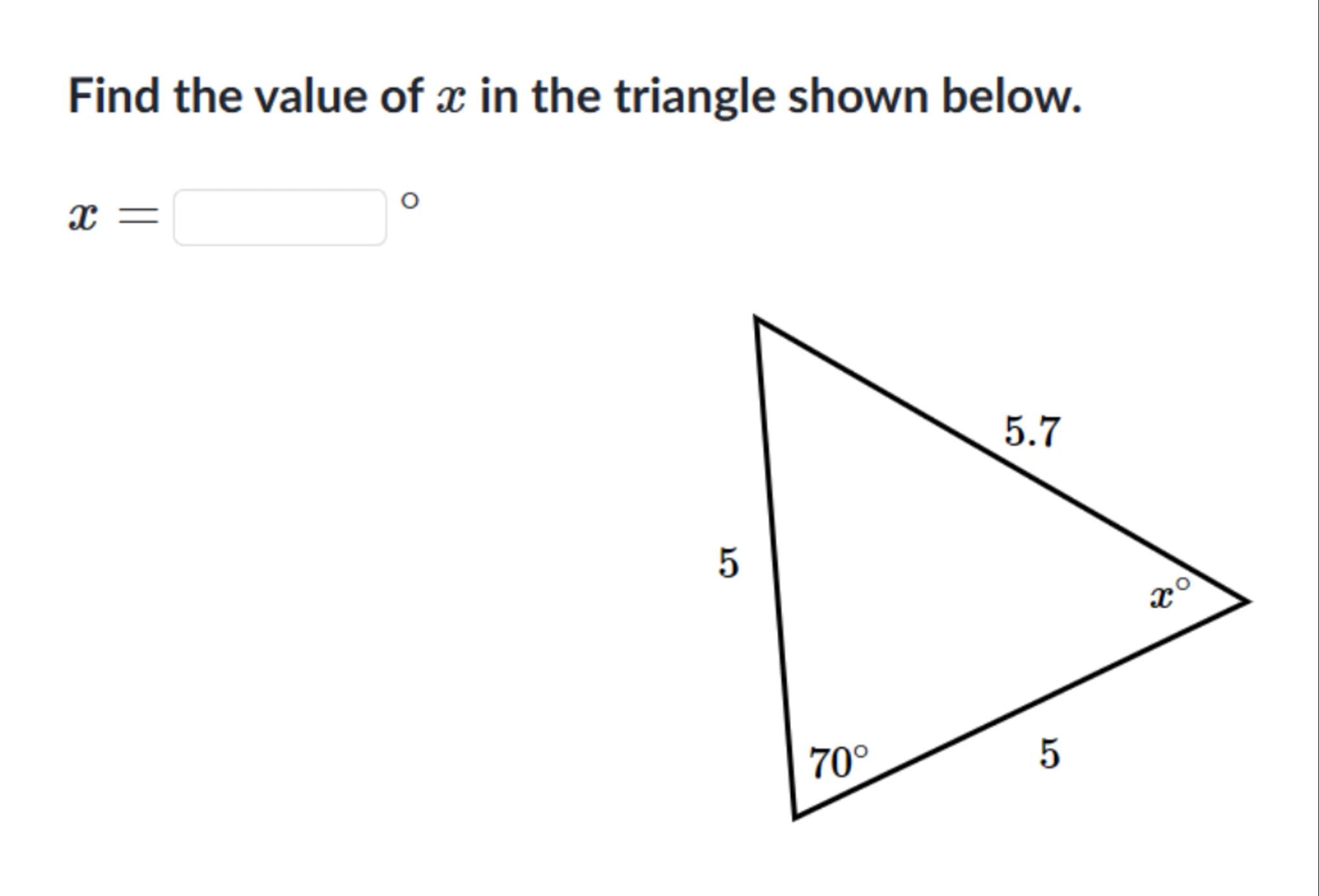

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Given a triangle with sides of length 5, 5, and 5.7, and one angle of 70 degrees, we must first check if such a triangle is possible using the triangle inequality theorem
step 2
The triangle inequality theorem states that the sum of the lengths of any two sides of a triangle must be greater than the length of the third side
step 3
Checking the given sides: 5 + 5 > 5.7 (True), 5 + 5.7 > 5 (True), and 5 + 5.7 > 5 (True). All conditions satisfy the triangle inequality theorem, so the triangle is possible
step 4
Since the triangle is possible, we can use the Law of Cosines to find the unknown angle x
step 5
The Law of Cosines states that for any triangle with sides a, b, and c, and opposite angles A, B, and C respectively:
step 6
Using the Law of Cosines with sides 5, 5, and 5.7, and the known angle of 70 degrees, we can solve for the angle opposite the side of length 5.7
step 7
Let's denote the sides as a = b = 5 and c = 5.7, and the angle opposite side c as A (which is 70 degrees). We can rearrange the Law of Cosines to solve for :
step 8
Plugging in the values:
step 9
Calculating the cosine value:
step 10
Since the cosine of an angle cannot be greater than 1, and the calculated value exceeds this, there is an inconsistency. This suggests that the initial information provided may be incorrect, or the triangle configuration as described is not possible
step 11
Referring back to the asksia-ll calculation list, it is stated that the triangle with the given dimensions and angle is not possible. Therefore, we cannot find the value of angle x as the triangle cannot exist
Answer
The triangle with sides 5, 5, and 5.7 and one angle of 70 degrees is not possible; hence, the value of angle x cannot be determined.
Key Concept
Triangle Inequality Theorem and Law of Cosines
Explanation
The Triangle Inequality Theorem helps determine the possibility of a triangle's existence based on its sides, and the Law of Cosines relates the lengths of the sides of a triangle to the cosine of one of its angles. However, if the initial conditions lead to an impossible triangle, as indicated by the asksia-ll calculation, no further calculations can be made to find the unknown angle.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question