
Sia

Question
Math
Posted over 1 year ago
Given the following Venn diagram, find .
58
54
20
17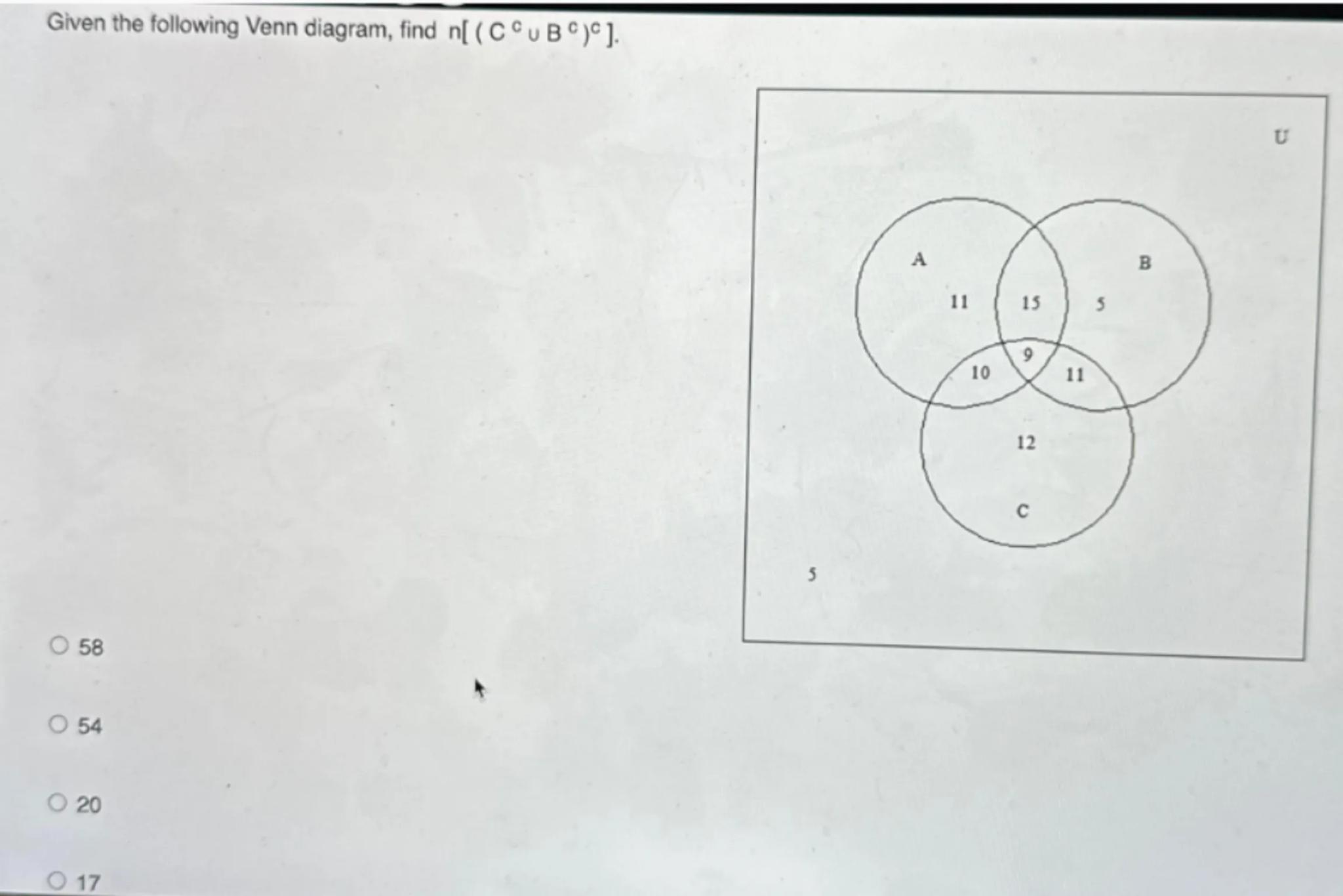

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Identify the sets and their elements from the Venn diagram. Set A: {11, 15, 10, 9}, Set B: {15, 5, 9, 11}, Set C: {10, 9, 11, 12}
step 2
Determine the elements in the complement of set C, . Since the universal set U is not fully specified, we assume it includes all elements mentioned: {5, 9, 10, 11, 12, 15}. Thus, = {5, 15}
step 3
Determine the elements in the complement of set B, . Using the same universal set, = {10, 12}
step 4
Find the union of the complements, . This results in the set {5, 10, 12, 15}
step 5
Find the complement of the union, . This includes all elements in the universal set U that are not in {5, 10, 12, 15}. Thus, = {9, 11}
step 6
Count the number of elements in . There are 2 elements: 9 and 11. Therefore,
Answer
2
Key Concept
Set Operations and Complements
Explanation
The problem involves finding the complement of the union of the complements of two sets within a universal set. This requires understanding and applying set operations and complements.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question