
Sia

Question
Math
Posted over 1 year ago
In the figure below, and are diameters of circle .
What is the arc measure of major arc B \overparen{D} C in degrees?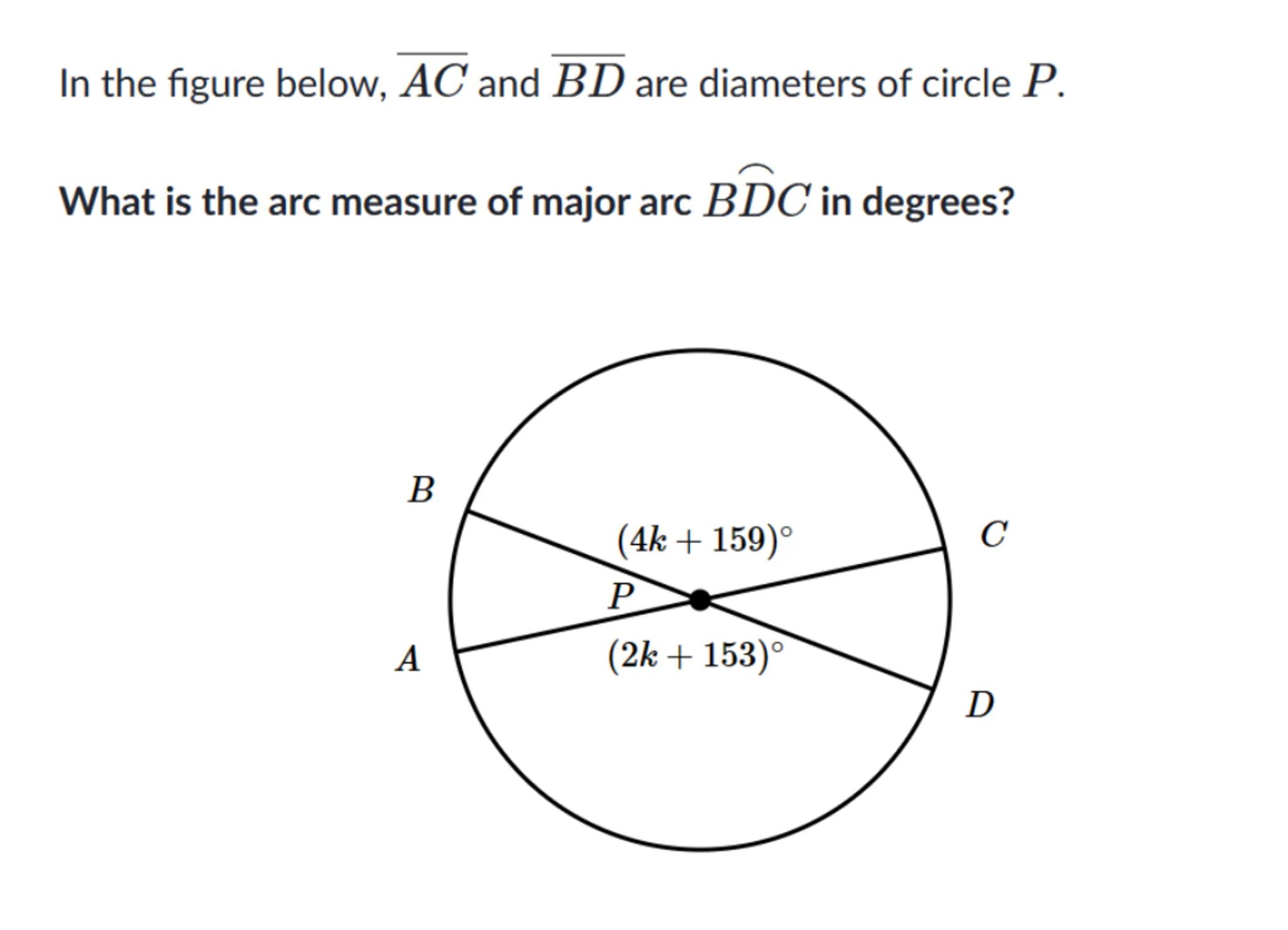

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Combine like terms in the equation
step 2
Simplify to get
step 3
Subtract 312 from both sides to isolate the term with , resulting in
step 4
Divide both sides by 6 to solve for , yielding
step 5
Substitute into the angle to find its measure: angle
step 6
Calculate the measure of angle by substituting : angle degrees
step 7
Since is a diameter, angle intercepts a semicircle, and thus the arc measure of B\overparen{D}C is degrees
[question 1] Answer
The arc measure of major arc B \overparen{D} C is degrees.
Key Concept
Intercepted Arc by a Central Angle
Explanation
The measure of an arc intercepted by a central angle is equal to the measure of the angle itself. Since angle intercepts a semicircle, the remaining arc B\overparen{D}C is the difference between degrees and the measure of angle .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question