
Sia

Question
Math
Posted over 1 year ago
Kadence took a random sample of 24 students at her school and asked them how much they typically slept on a school night versus a weekend night. Here is computer output from a least-squares regression analysis on her sample:
Regression: weekend vs. school night
\begin{tabular}{lrr}
Predictor & Coef & SE Coef \\
\hline Constant & 3.182 & 2.319 \\
School night & 0.789 & 0.237 \\
S & R-sq &
\end{tabular}
Assume that all conditions for inference have been met.
Which of these is an appropriate test statistic for testing the null hypothesis that the population slope in this setting is 0 ?
Choose 1 answer:
(A)
(B)
(C)
()
(E) 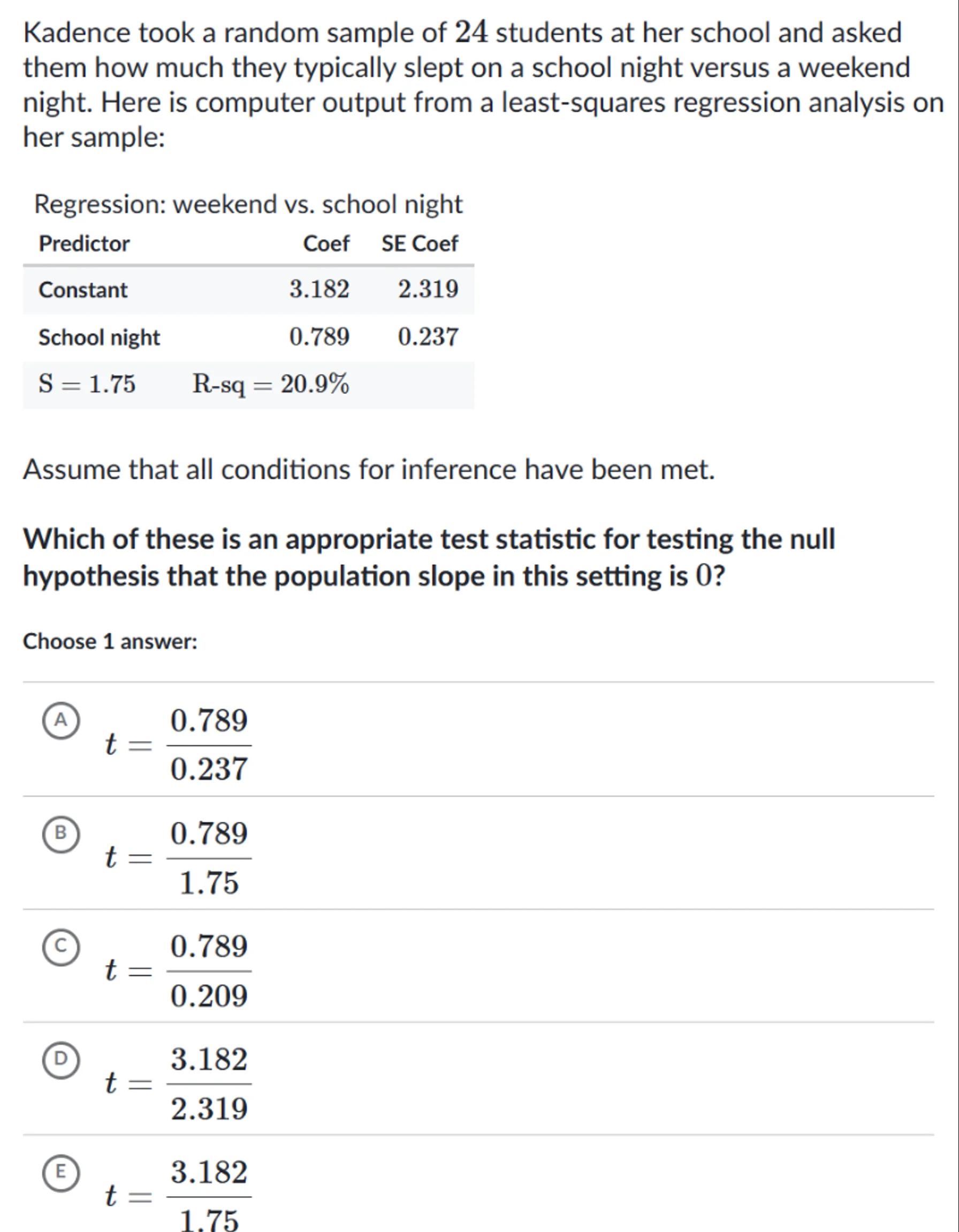

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
The estimate of the slope is the coefficient of "School night", which is 0.789
step 3
The null value of the slope we are testing against is 0
step 4
The standard error (SE) of the slope estimate is 0.237
step 5
Plugging the values into the t-statistic formula gives us
step 6
Calculating the t-statistic, we get
step 7
Using the asksia-ll calculator result, the calculation is
step 8
The t-statistic is approximately 3.33
1 Answer
A
Key Concept
t-statistic for hypothesis testing
Explanation
The t-statistic is used to determine if there is a significant difference between the estimated parameter and the null hypothesis value, taking into account the variability of the estimate as measured by its standard error.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question