
Sia

Question
Math
Posted over 1 year ago
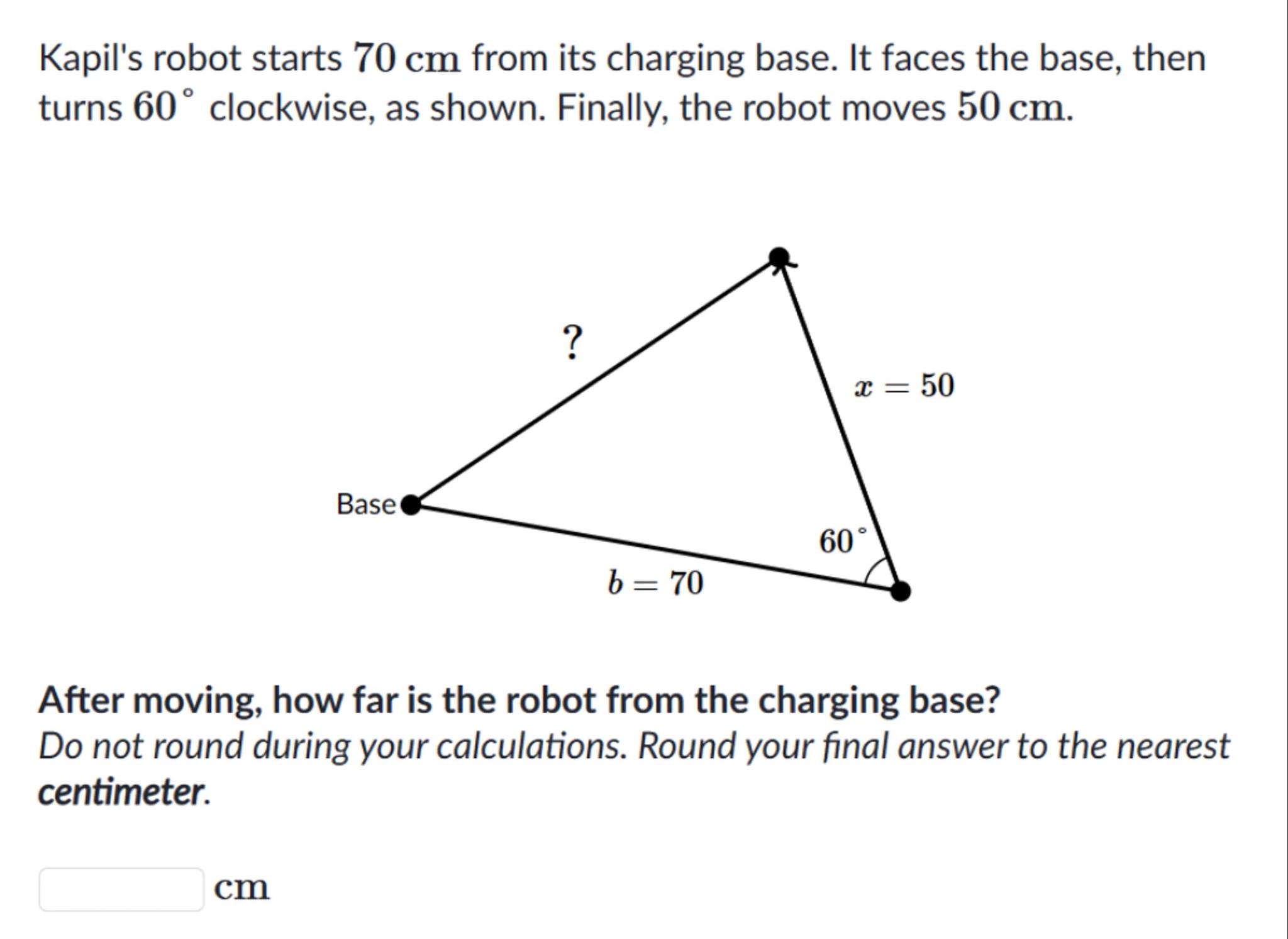
Kapil's robot starts from its charging base. It faces the base, then turns clockwise, as shown. Finally, the robot moves .
After moving, how far is the robot from the charging base?
Do not round during your calculations. Round your final answer to the nearest centimeter.

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find the unknown side of the triangle, we can use the Law of Cosines since we have two sides and the included angle
step 2
The Law of Cosines formula is , where and are the sides and is the included angle
step 3
Substitute the given values into the Law of Cosines formula:
step 4
Calculate the cosine of , which is
step 5
Substitute the cosine value into the equation:
step 6
Perform the arithmetic:
step 7
Simplify the equation:
step 8
Take the square root of both sides to find :
step 9
Calculate the square root: cm
step 10
Round the final answer to the nearest centimeter: cm
Answer
62 cm
Key Concept
Law of Cosines
Explanation
The Law of Cosines is used to find an unknown side of a triangle when two sides and the included angle are known. It is especially useful in non-right triangles.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question