
Sia

Question
Math
Posted over 1 year ago
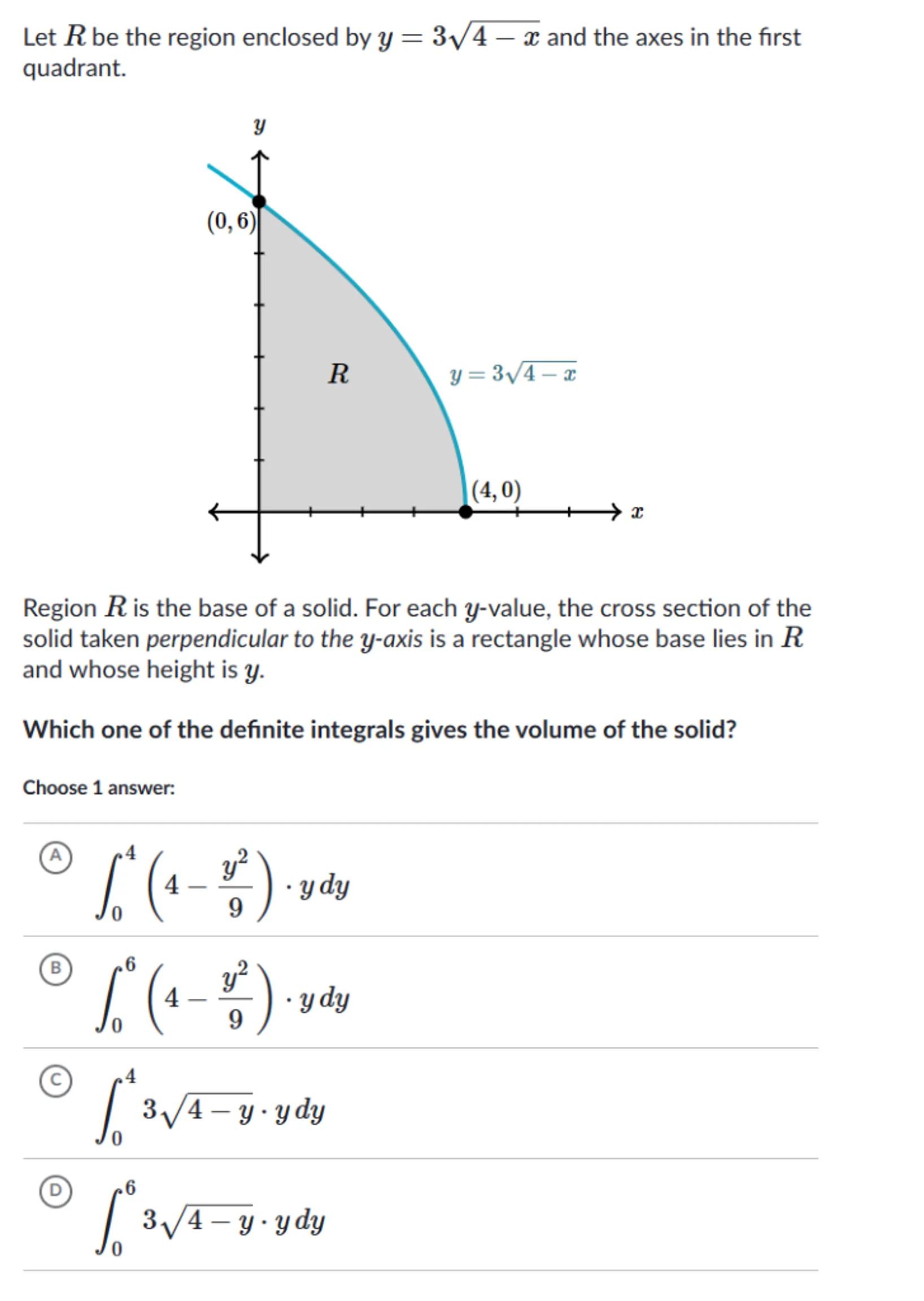
Let be the region enclosed by and the axes in the first quadrant.
Region is the base of a solid. For each -value, the cross section of the solid taken perpendicular to the -axis is a rectangle whose base lies in and whose height is .
Which one of the definite integrals gives the volume of the solid?
Choose 1 answer:
(A)
(B)
(c)
() 

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
The cross-section of the solid perpendicular to the y-axis is a rectangle with base in and height
step 3
The base of the rectangle at a given is the horizontal distance from the y-axis to the curve, which is
step 4
The volume of the solid is given by the integral of the area of the cross-section along the y-axis. The area of the cross-section is
step 5
The correct integral to find the volume is
D
Key Concept
Volume of a solid with cross-sectional area
Explanation
The volume of a solid can be found by integrating the area of its cross-sections along the axis perpendicular to the cross-sections.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question