
Sia

Question
Math
Posted over 1 year ago
Let be the function defined by the rule .
(a) Find the domain of . (Enter your answer using interval notation.)
(b) Compute for .
(c) Use the results obtained in parts (a) and (b) to sketch the graph of .
(i)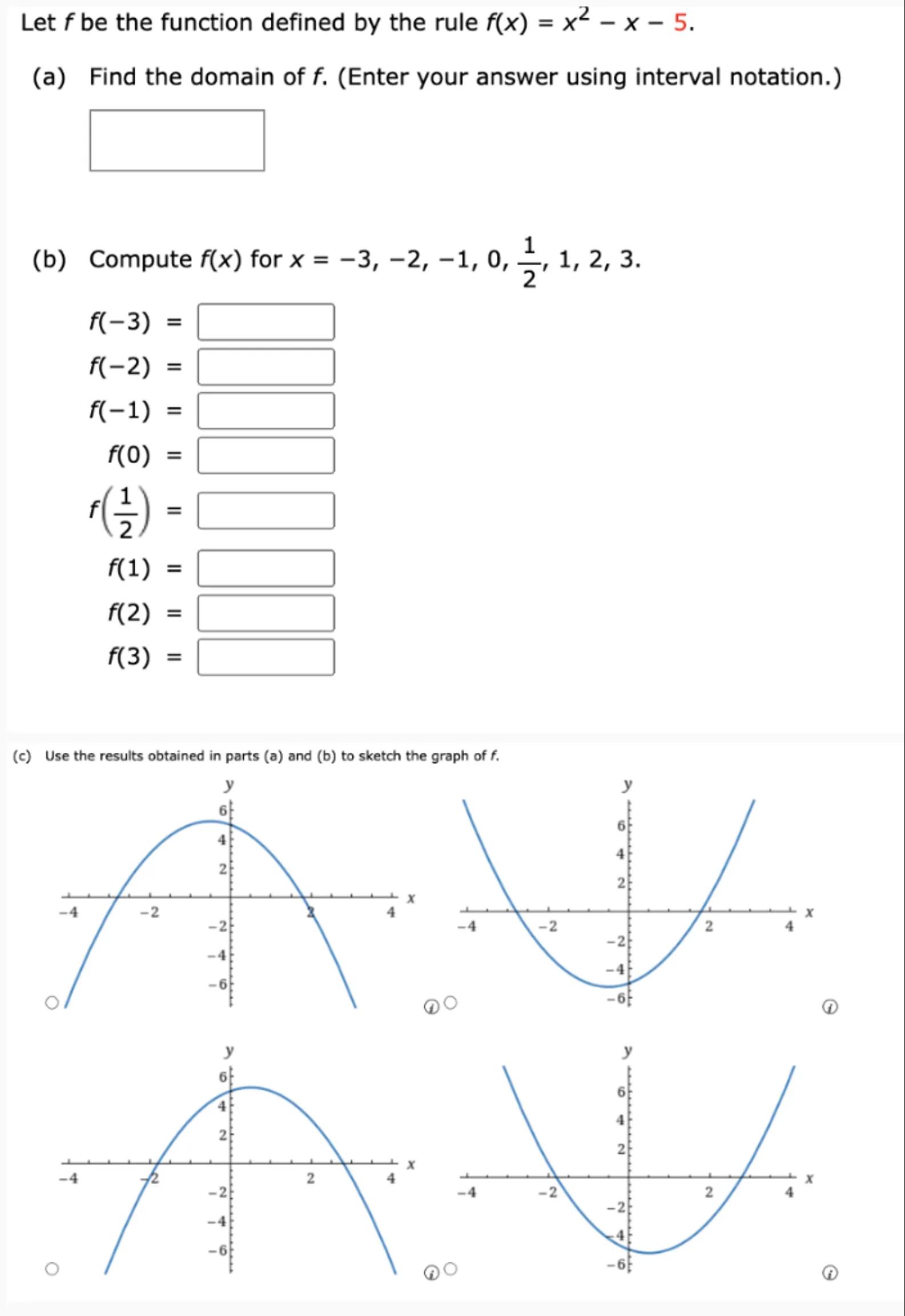

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find the domain of the function , we note that it is a polynomial function. Polynomial functions are defined for all real numbers. Therefore, the domain of is all real numbers
step 2
To compute for , we substitute each value of into the function
step 3
For :
step 4
For :
step 5
For :
step 6
For :
step 7
For :
step 8
For :
step 9
For :
step 10
For :
step 11
Using the results from steps 3 to 10, we can sketch the graph of . The points to plot are: , , , , , , ,
Answer
The domain of is all real numbers. The computed values are , , , , , , , . The graph can be sketched using these points.
Key Concept
Domain and range of polynomial functions
Explanation
Polynomial functions are defined for all real numbers, and their graphs can be sketched by plotting points obtained from evaluating the function at specific values of .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question