
Sia

Question
Math
Posted over 1 year ago
Let be a twice differentiable function except at a vertical asymptote. One of these graphs is the graph of , one is of and one is of .
Choose the option that matches each function with its appropriate graph.
Choose 1 answer:
(A) A
I II III
(B)
I III II
(C)
II III I
(D)
\begin{tabular}{|llll|}
\hline & & & \\
\hline & III & II & I \\
&
\end{tabular}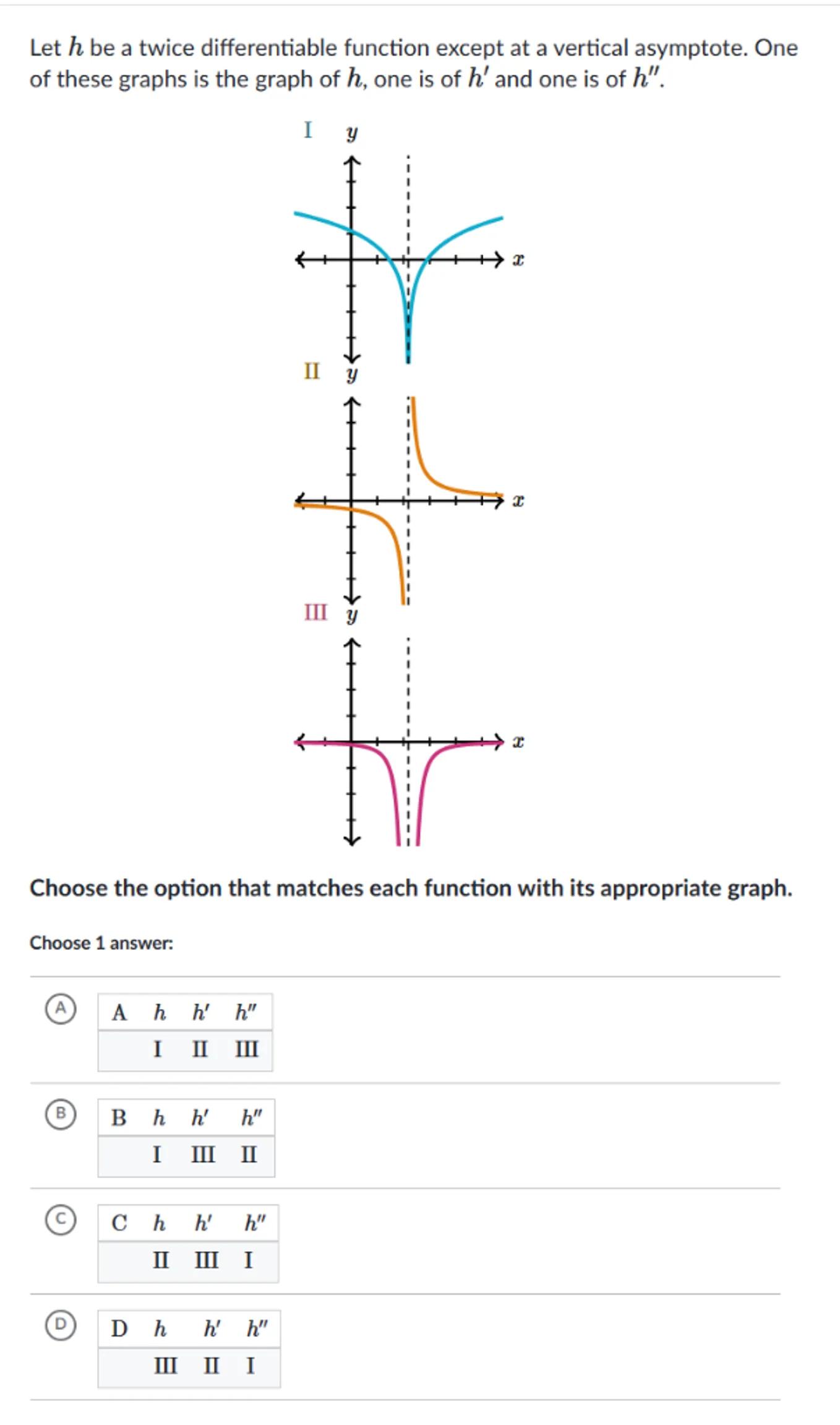

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
Graph I: The curve decreases, passes through the y-axis, continues to decrease until it gets close to the vertical asymptote, then increases after the asymptote. This behavior suggests it could be the original function
step 3
Graph II: The curve increases, passes through the y-axis, continues to increase until it gets close to the vertical asymptote, then decreases after the asymptote. This behavior suggests it could be the first derivative
step 4
Graph III: The curve decreases, continues to decrease until it gets close to the vertical asymptote, then decreases again after the asymptote. This behavior suggests it could be the second derivative
step 5
Match the graphs to the functions: corresponds to Graph I, corresponds to Graph II, and corresponds to Graph III
A
Key Concept
Matching functions and their derivatives to graphs
Explanation
By analyzing the behavior of each graph, we can determine which graph represents the original function, its first derivative, and its second derivative.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question