
Sia

Question
Math
Posted about 1 year ago
Manny's burrito stand lets customers choose 4 ingredients from the list below to add their burritos:
\begin{tabular}{|c|c|c|c|}
\hline Onions & Cilantro & Jalapeño & Beans \\
\hline Cheese & Crema & Salsa & Hot sauce \\
\hline
\end{tabular}
How many groups of 4 different ingredients can go on a burrito?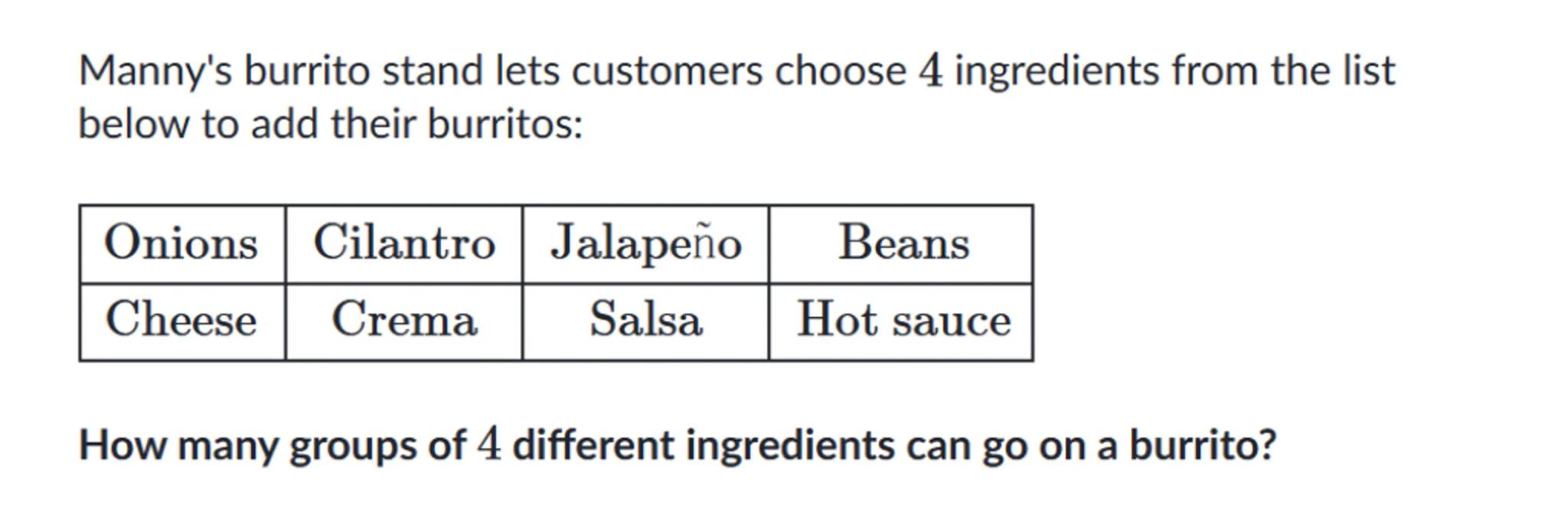

Answer from Sia
Posted about 1 year ago
Solution by Steps
step 1
To determine the number of different groups of 4 ingredients that can be chosen from 8 ingredients, we use the binomial coefficient
step 2
The binomial coefficient formula is , where is the total number of items, and is the number of items to choose
step 3
Applying the formula with and , we get
step 4
Simplifying the expression, we have
step 5
Calculating the simplified expression gives us
Answer
There are 70 different groups of 4 ingredients that can go on a burrito.
Key Concept
Combinations and the Binomial Coefficient
Explanation
The number of ways to choose items from a set of distinct items is given by the binomial coefficient , which is calculated using the formula . This represents the number of combinations possible without regard to order.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question