
Sia

Question
Math
Posted over 1 year ago
Mark constructed parallel to through point
Which of the following statements best justifies why is parallel to
Choose 1 answer:
(A) Lines perpendicular to the same transversal are parallel.
(B) Lines with congruent same-side interior angles are parallel.
(C) Lines with congruent alternate interior angles are parallel.
(D) Lines with congruent corresponding angles are parallel.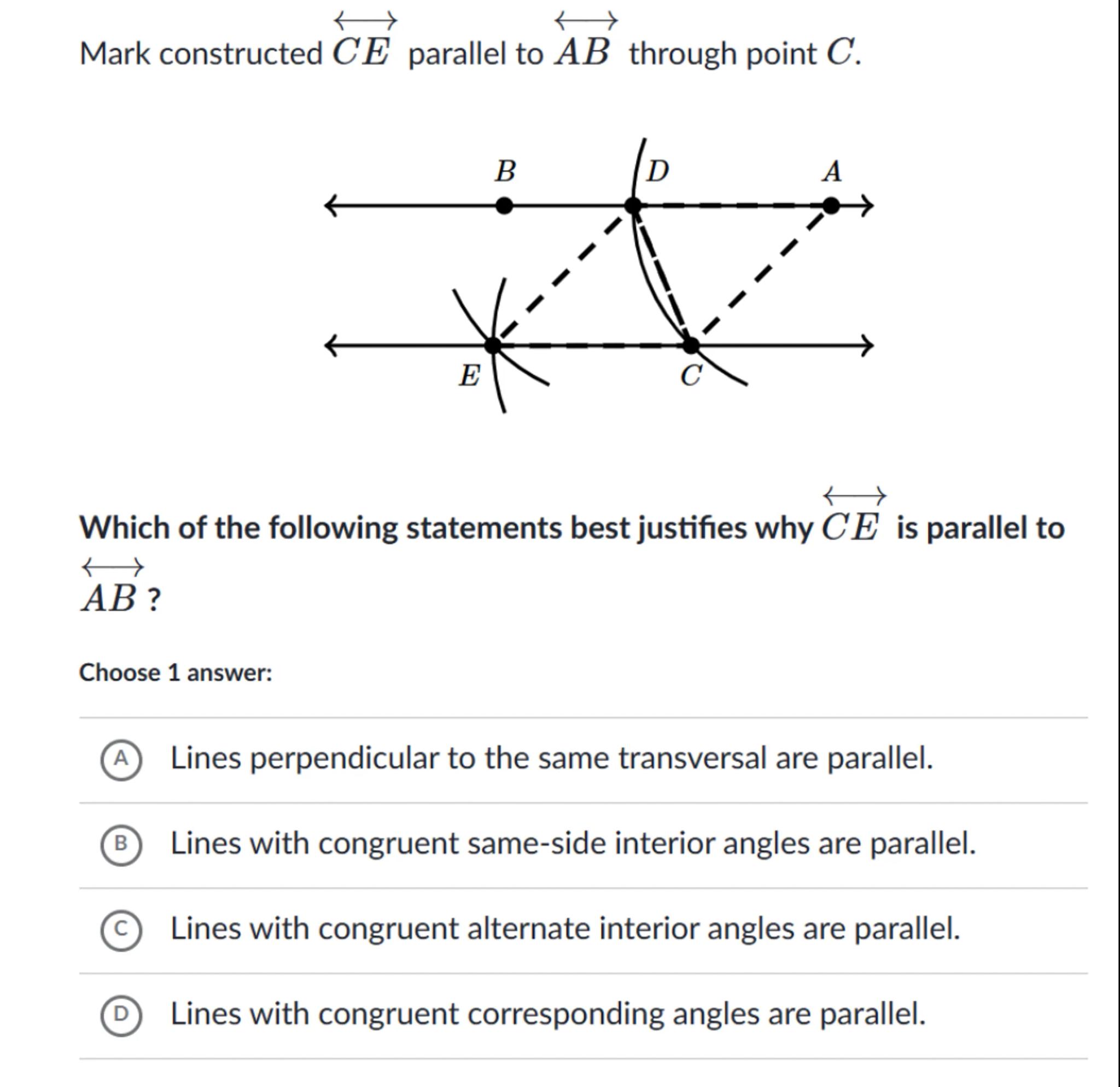

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Given that line is constructed parallel to line through point , we need to identify the statement that justifies this parallelism
step 2
From the given information and the diagram, we can infer that the lines are parallel by definition, as it is stated that line is constructed to be parallel to line
step 3
However, to choose the best answer from the given options, we need to consider the properties of parallel lines and the corresponding angles they form with a transversal
step 4
If two lines are cut by a transversal and the corresponding angles are congruent, then the lines are parallel. This is a property of parallel lines
step 5
Since line acts as a transversal for lines and , and the corresponding angles formed would be congruent by the construction of parallel lines, the correct justification is that lines with congruent corresponding angles are parallel
Answer
(D) Lines with congruent corresponding angles are parallel.
Key Concept
Corresponding Angles Postulate
Explanation
When two lines are cut by a transversal, if the corresponding angles are congruent, the lines are parallel. This is known as the Corresponding Angles Postulate.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question