
Sia

Question
Math
Posted over 1 year ago
Multiply.
Simplify your answer as much as possible.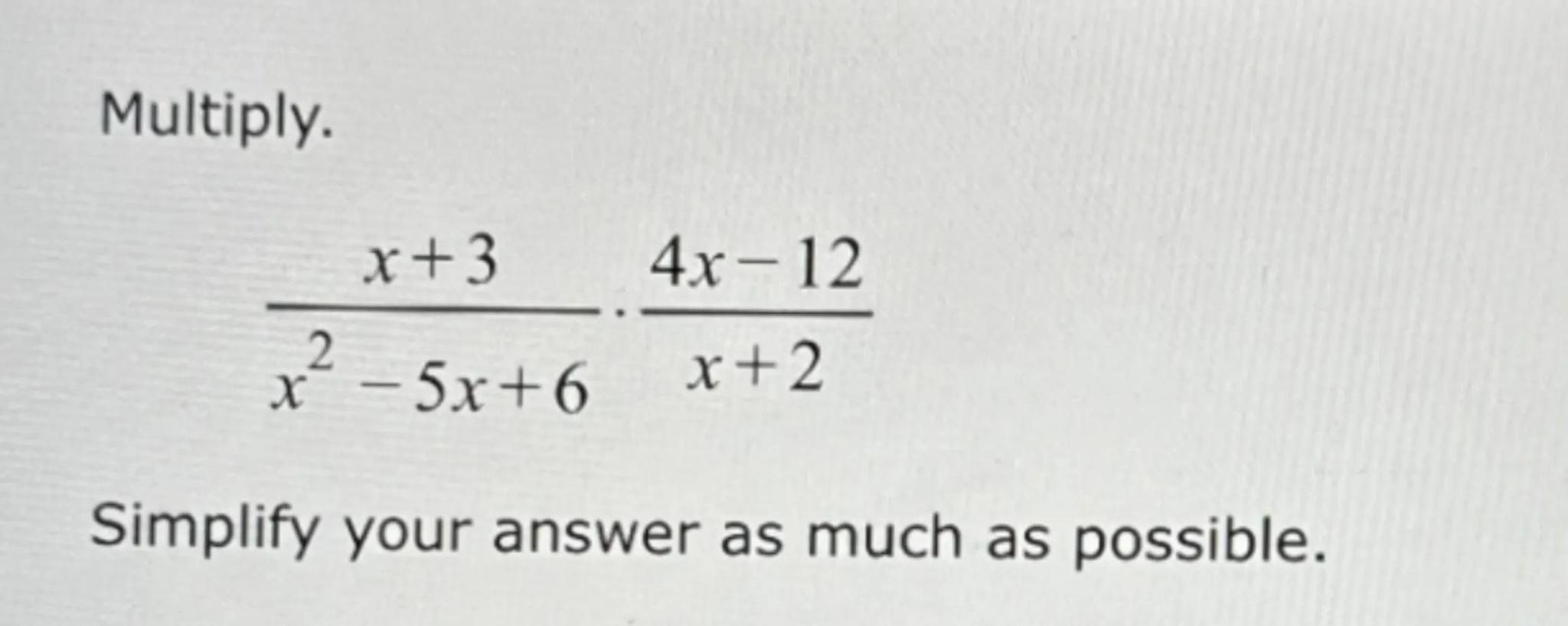

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
First, factor the denominators and numerators where possible. The expression is:
step 2
Factor the quadratic expression in the denominator:
step 3
Substitute the factored form into the expression:
step 4
Simplify the numerator :
step 5
Substitute the simplified numerator:
step 6
Cancel out the common factors :
step 7
Multiply the remaining fractions:
step 8
Simplify the final expression:
Answer
Key Concept
Simplification of Rational Expressions
Explanation
The key concept here is to factor both the numerator and the denominator where possible, cancel out common factors, and then simplify the resulting expression.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question