Asksia AI LOGO

Sia

Question
Math
Posted 9 months ago

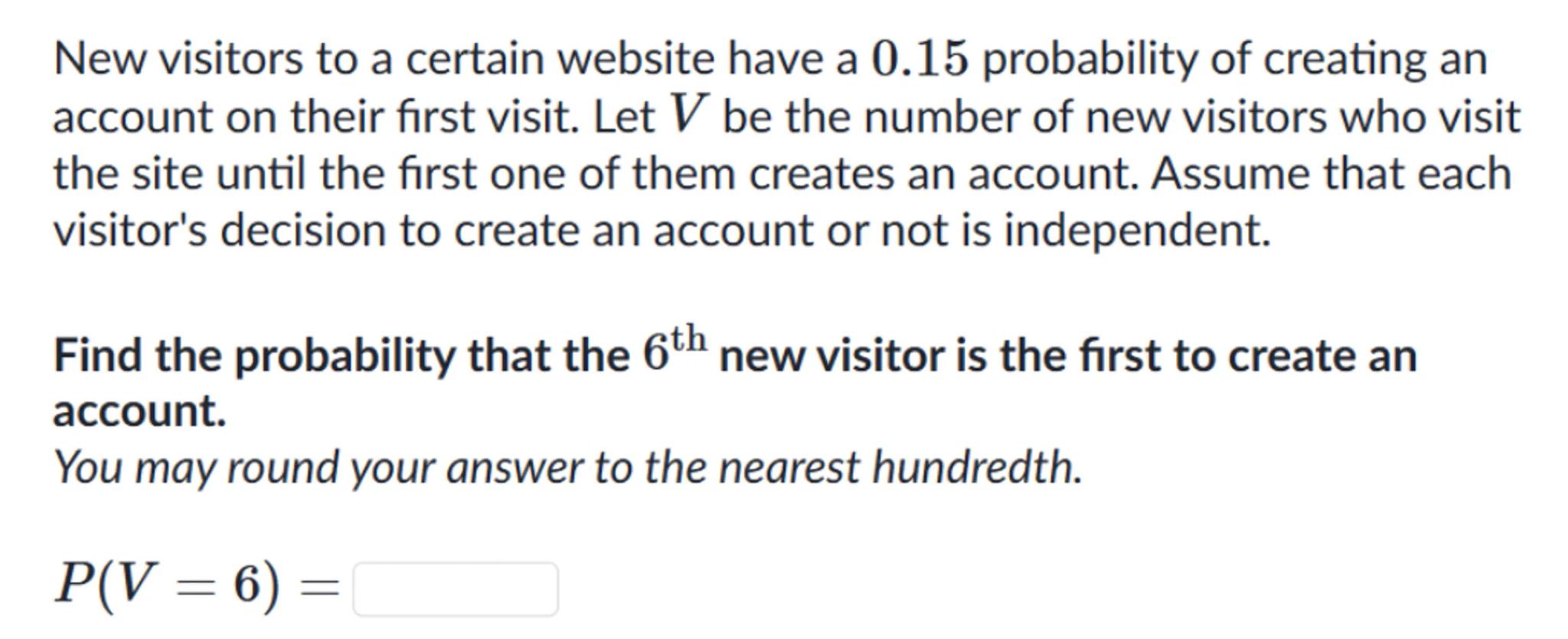
New visitors to a certain website have a 0.15 probability of creating an account on their first visit. Let VV be the number of new visitors who visit the site until the first one of them creates an account. Assume that each visitor's decision to create an account or not is independent.

Find the probability that the 6th 6^{\text {th }} new visitor is the first to create an account.
You may round your answer to the nearest hundredth.
P(V=6)=
P(V=6)=
Sign in to unlock the answer
Answer from Sia
Posted 9 months ago
Solution by Steps
step 1
To find the probability that the 6th new visitor is the first to create an account, we use the geometric distribution formula: P(V=k)=(1−p)k−1pP(V=k) = (1-p)^{k-1}p, where pp is the probability of success on any given trial, and kk is the number of trials until the first success
step 2
In this case, p=0.15p=0.15 is the probability of a new visitor creating an account, and k=6k=6 is the number of visitors until the first account creation
step 3
Substitute pp and kk into the formula: P(V=6)=(1−0.15)6−1×0.15P(V=6) = (1-0.15)^{6-1} \times 0.15
step 4
Calculate the probability: P(V=6)=(0.85)5×0.15P(V=6) = (0.85)^5 \times 0.15
step 5
Using the asksia-ll calculation list, we have the result: P(V=6)=(0.85)5×0.15=0.067P(V=6) = (0.85)^5 \times 0.15 = 0.067
Answer
P(V=6)=0.067P(V=6) = 0.067
Key Concept
Geometric Distribution
Explanation
The geometric distribution is used to model the number of trials until the first success in a series of independent Bernoulli trials, where each trial has the same probability of success.

Not the question you are looking for? Ask here!

Enter question by text

Enter question by image

Unlock Smarter Learning with AskSia Super!

Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.

30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question