
Sia

Question
Math
Posted over 1 year ago
On the following unit circle, is in radians and .
Without a calculator, evaluate the following expressions to the nearest hundredth or as an exact ratio.
\begin{tabular}{ll}
Expression & Value \\
\hline & \\
&
\end{tabular}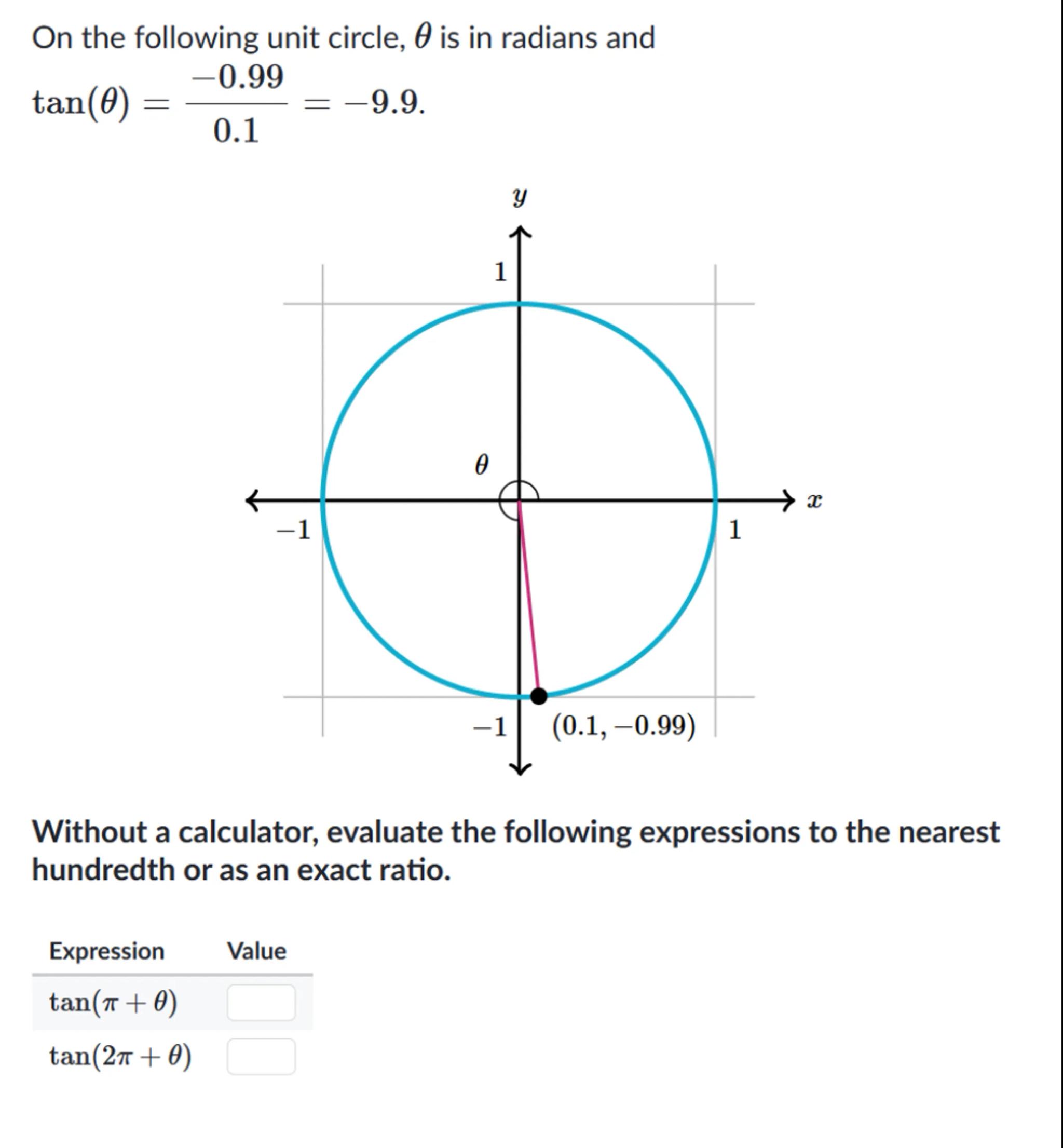

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find , we use the periodic property of the tangent function, which states that
step 2
Since , we have
1 Answer
step 1
To find , we use the periodic property of the tangent function, which states that
step 2
Since , we have
2 Answer
Key Concept
Periodicity of the Tangent Function
Explanation
The tangent function is periodic with a period of , which means for any integer . Therefore, and both simplify to .
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question