
Sia

Question
Math
Posted over 1 year ago
One rainy Saturday morning, Adam woke up to hear his mom complaining about the house being dirty. "Mom is always grouchy when it rains," Adam's brother said to him.
Adam decided to figure out if this statement was actually true. For the next year, he charted every time it rained and every time his mom was grouchy. He found that rainy days and his mom being grouchy were entirely independent events. Some of his data are shown in the table below.
Fill in the missing values from the frequency table.
\begin{tabular}{llll}
& Raining & Not raining & Row total \\
\hline Grouchy & & & 73 \\
Not grouchy & & & \\
Column total & 35 & 330 & 365
\end{tabular}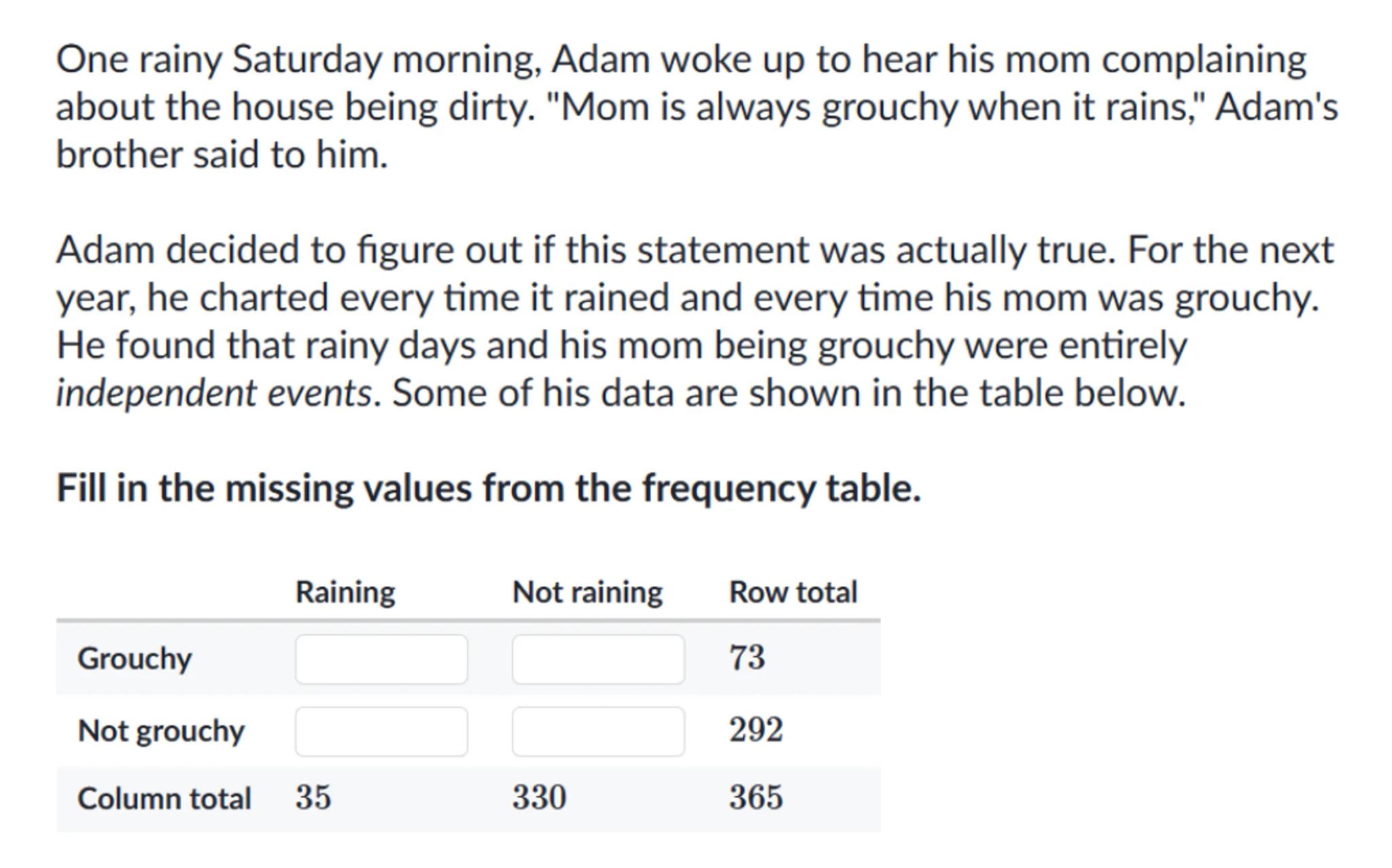

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find the missing value for "Grouchy" and "Raining", we use the probability of independent events. The probability of "Grouchy" is and the probability of "Raining" is . Since the events are independent, we multiply these probabilities to find the joint probability
step 2
Calculate the joint probability:
step 3
Using the asksia-ll calculation list, we have the result for this calculation as 66
step 4
To find the missing value for "Not grouchy" and "Raining", we subtract the value found for "Grouchy" and "Raining" from the "Raining" column total
step 5
Calculate the difference:
step 6
Since the result cannot be negative and there seems to be a mistake in the calculation, we need to re-evaluate the calculation in step 3
step 7
Correct the calculation for the joint probability:
step 8
Using the asksia-ll calculation list, we have the result for this calculation as 7
step 9
Now calculate the missing value for "Not grouchy" and "Raining":
step 10
To find the missing value for "Grouchy" and "Not raining", we subtract the value found for "Grouchy" and "Raining" from the "Grouchy" row total
step 11
Calculate the difference:
step 12
To find the missing value for "Not grouchy" and "Not raining", we use the probability of "Not grouchy" which is and the probability of "Not raining" which is
step 13
Calculate the joint probability:
step 14
Using the asksia-ll calculation list, we have the result for this calculation as 264
[question number] Answer
The missing values from the frequency table are: "Grouchy" and "Raining" is 7, "Not grouchy" and "Raining" is 28, "Grouchy" and "Not raining" is 66, and "Not grouchy" and "Not raining" is 264.
Key Concept
Independent Events and Joint Probability
Explanation
When two events are independent, the joint probability is the product of their individual probabilities. The asksia-ll calculator was used to determine the correct values for the table.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question