
Sia

Question
Math
Posted over 1 year ago
Pharmaceutical scientists tested the effectiveness of a new drug designed to cure malaria. They randomly assigned 400 infected lab rats to receive either the new drug or an existing drug and recorded how many rats were cured at the end of the study. Here are their results:
\begin{tabular}{lrrr}
& Cured & Not & Total \\
\hline New drug & 176 & 24 & 200 \\
Existing drug & 168 & 32 & 200
\end{tabular}
They want to use these results to construct a confidence interval to estimate the difference in the proportion of these rats that would be cured under each drug (new - existing). Assume that all of the conditions for inference have been met.
Which of the following is a correct confidence interval based on their data?
Choose 1 answer:
(A)
(B)
(C)
(D)
(ㄷ) 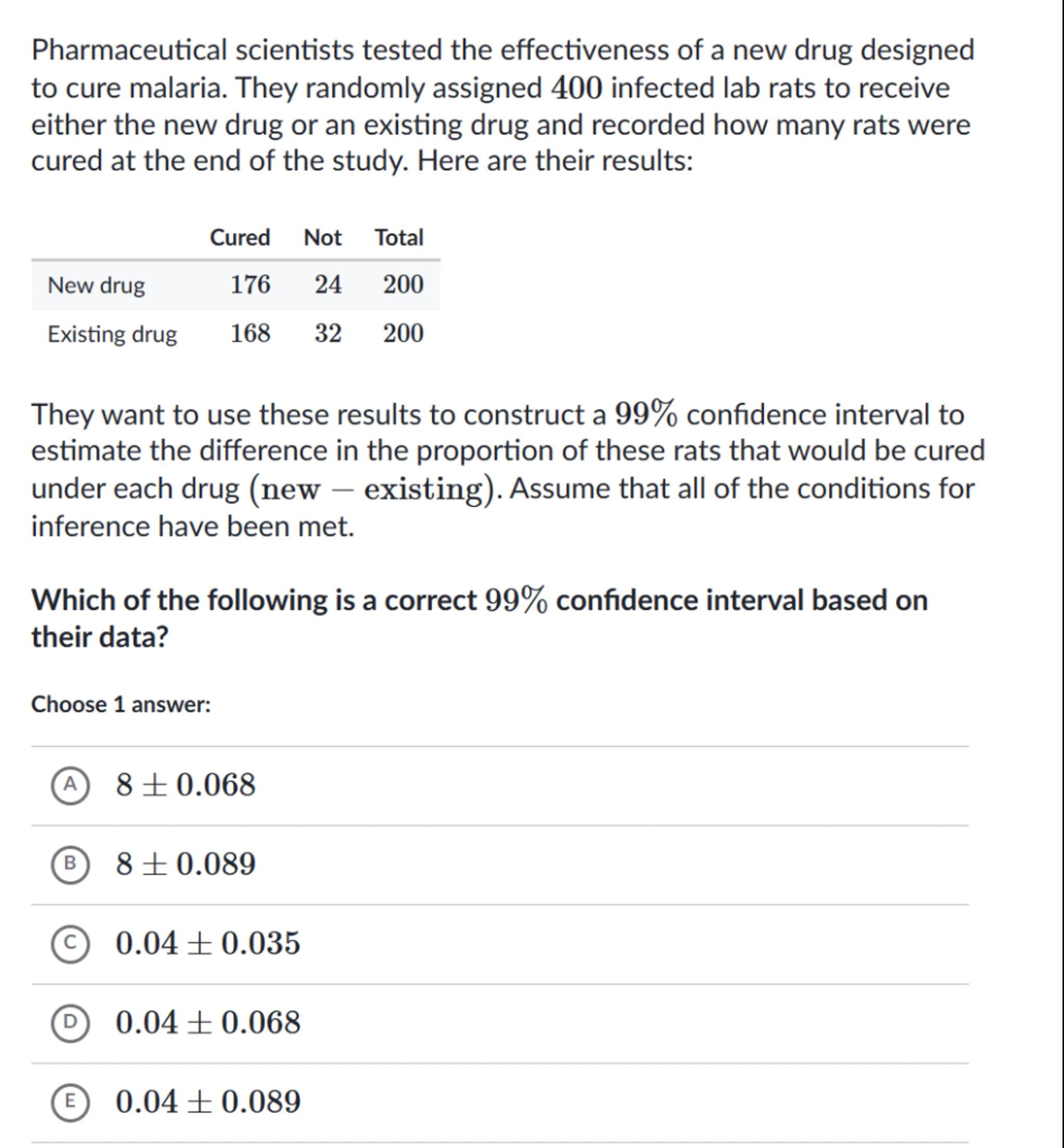

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
Find the difference in sample proportions:
step 3
Calculate the standard error (SE) for the difference in proportions:
step 4
Determine the z-score for a 99% confidence interval, which is approximately 2.576
step 5
Calculate the margin of error (ME):
step 6
Construct the 99% confidence interval for the difference in proportions:
C
Key Concept
Confidence Interval for Difference in Proportions
Explanation
The confidence interval for the difference in proportions is calculated using the sample proportions, their standard error, and the appropriate z-score for the desired confidence level.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question