
Sia

Question
Math
Posted over 1 year ago
Point is the image of under a translation.
Determine the translation.
Use non-negative numbers.
A translation by units to the right/left and units
up/down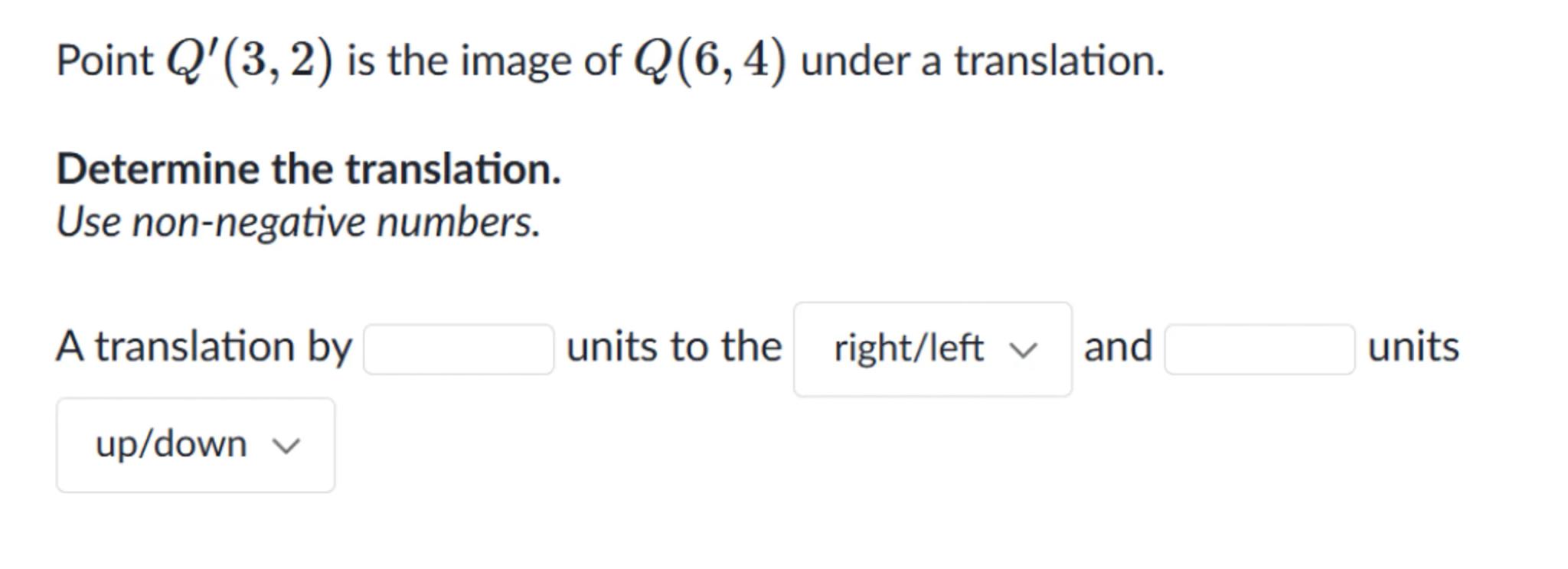

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
Identify the original coordinates of point and the translated coordinates of point
step 2
Calculate the change in the -coordinate from to by subtracting the -coordinate of from the -coordinate of :
step 3
Calculate the change in the -coordinate from to by subtracting the -coordinate of from the -coordinate of :
step 4
Determine the direction of the translation for both and coordinates based on the signs of the changes calculated in steps 2 and 3
Answer
The translation is 3 units to the left and 2 units down.
Key Concept
Translation in the Coordinate Plane
Explanation
To find the translation that maps point to point , we subtract the coordinates of from the coordinates of . The result gives us the magnitude and direction of the translation. A positive result indicates a translation to the right (for ) or up (for ), while a negative result indicates a translation to the left (for ) or down (for ). In this case, the translation is to the left and down because the changes in coordinates are negative.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question