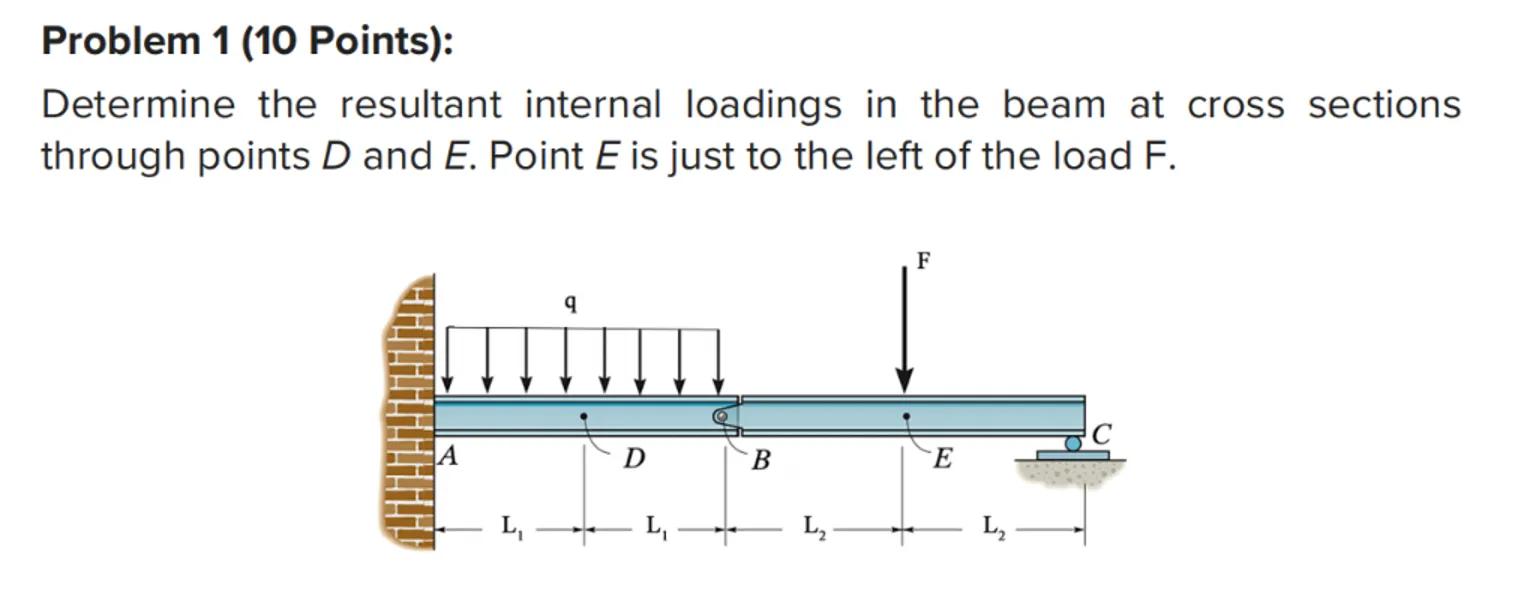
Problem 1 (10 Points):
Determine the resultant internal loadings in the beam at cross sections through points $D$ and $E$. Point $E$ is just to the left of the load $F$.

Question

Accepted Answer

∻Solution∻ ‖ a ⋮ To determine the resultant internal loadings at section D, we first need to calculate the reactions at the supports. The total distributed load on the beam is given by the formula $$W = q \cdot (L_1 + L_2) = 2 \, ext{kN/m} \cdot (5 \, ext{m} + 8 \, ext{m}) = 26 \, ext{kN}$$. The point load $F$ is 14 kN. We can use the equilibrium equations to find the reactions at supports A and C. ‖ ‖ b ⋮ Using the moment about point A to find the reaction at C, we have: $$\sum M_A = 0 \Rightarrow R_C \cdot (L_1 + L_2) - W \cdot \left(\frac{L_1 + L_2}{2} ight) - F \cdot (L_1 + L_2 - 5) = 0$$. Substituting the values, we can solve for $R_C$. ‖ ‖ c ⋮ After finding $R_C$, we can use the vertical force equilibrium equation $$\sum F_y = 0 \Rightarrow R_A + R_C - W - F = 0$$ to find the reaction at support A. ‖ ‖ d ⋮ Now, to find the internal loadings at section D, we consider the left side of the section. The internal shear force $V_D$ can be calculated as $$V_D = R_A - W_{left}$$, where $W_{left}$ is the total load to the left of section D. ‖ ‖ e ⋮ For section E, just to the left of the point load F, the internal shear force $V_E$ will be $$V_E = V_D - F$$. The internal bending moment at section D can be calculated using $$M_D = R_A \cdot d - W_{left} \cdot \left(\frac{L_1}{2} ight)$$, and for section E, $$M_E = M_D - F \cdot (L_1 + L_2 - 5)$$. ‖ ∻Answer∻ ⚹ Resultant internal loadings at section D and E can be calculated using equilibrium equations and considering the loads acting on the beam. ⚹ ∻Key Concept∻ ⚹ Static Equilibrium: The sum of forces and moments acting on a beam must be zero for it to be in equilibrium. Equations: $$\sum F = 0$$ and $$\sum M = 0$$. ⚹ ∻Explanation∻ ⚹ By applying the principles of static equilibrium, we can determine the reactions at the supports and subsequently find the internal loadings at the specified sections of the beam. ⚹

Sia