
Sia
Q2. If the Beam A shown here had Section 1, what is the highest stress at the top and bottom of the cross section? Are they tensions or compressions?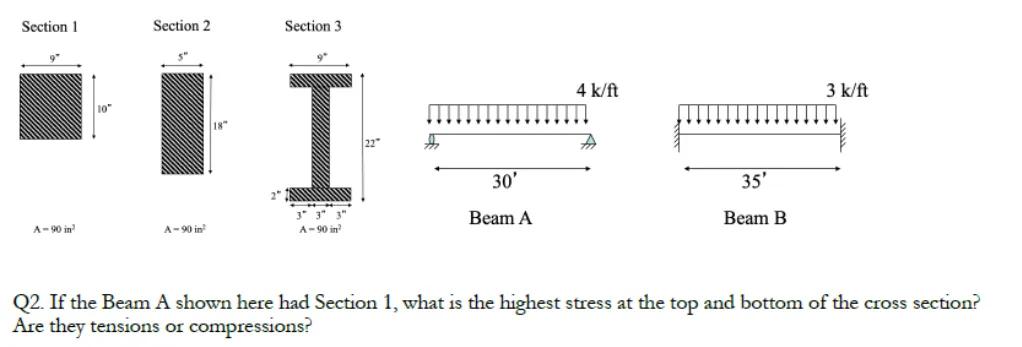

Answer from Sia
Posted over 1 year ago
Solution
a
To find the highest stress at the top and bottom of the cross-section for Beam A with Section 1, we first need to calculate the total load on the beam. The uniformly distributed load (w) is given as 4 kilopounds per foot, and the length of Beam A is 30 feet. Thus, the total load (W) can be calculated as:
b
The maximum bending moment (M) occurs at the center of the beam and can be calculated using the formula for a simply supported beam with a uniformly distributed load:
c
The moment of inertia (I) for Section 1 (a square cross-section) is given by the formula: , where both the width (b) and height (h) are 9 inches. Converting inches to feet, we have: . Thus,
d
The stress (σ) at the top and bottom of the cross-section can be calculated using the bending stress formula: , where c is the distance from the neutral axis to the outermost fiber. For a square section, . Therefore, . The top of the beam experiences compression, while the bottom experiences tension
D
Answer
The highest stress at the top is 4785.23 psi (compression), and at the bottom is 4785.23 psi (tension).
Key Concept
Bending Stress in Beams: The bending stress in a beam is calculated using the formula , where is the bending moment, is the distance from the neutral axis to the outermost fiber, and is the moment of inertia of the cross-section.
Explanation
The calculation of bending stress allows us to determine the maximum stress experienced by the beam under a given load, indicating whether the material is in tension or compression.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question