
Sia

Question
Math
Posted over 1 year ago
Quadrilateral is the result of dilating quadrilateral about point by a scale factor of .
Determine whether each claim about the properties of and is true or false.
The perimeters of and are the same.
True/false
The lengths of and are equal.
True/false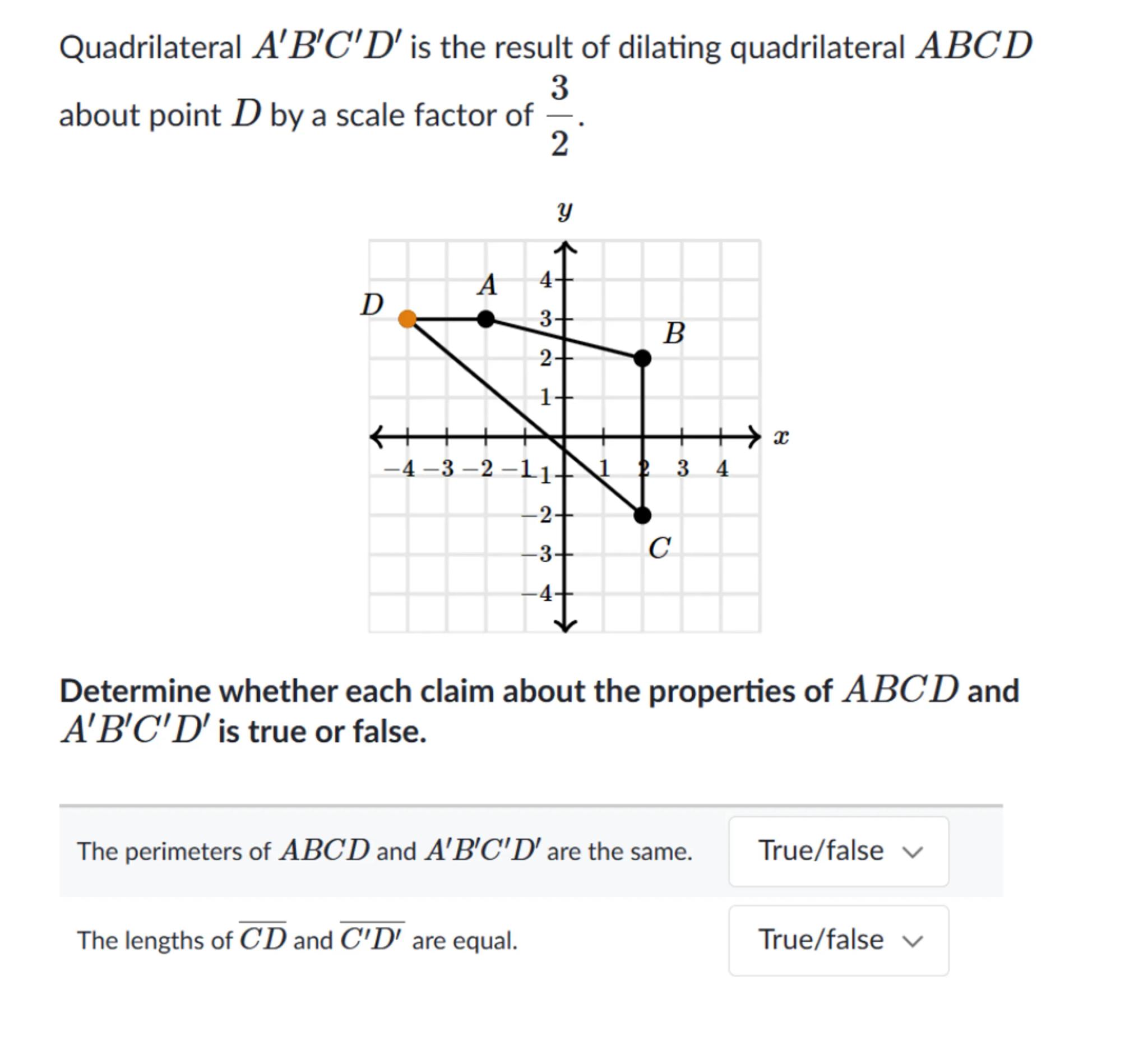

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 2
The perimeter of the original quadrilateral ABCD can be found by adding the distances between consecutive vertices. From the asksia-ll calculator, we have the distances as , , , and
step 3
The perimeter of ABCD is
step 4
To find the perimeter of the dilated quadrilateral A'B'C'D', we multiply each side of ABCD by the scale factor . Thus, the perimeter of A'B'C'D' is
step 5
Simplifying the expression for the perimeter of A'B'C'D', we get . Therefore, the perimeters of ABCD and A'B'C'D' are not the same
step 6
For the second statement, the length of CD is the distance between points C and D, which is
step 7
The length of C'D' after dilation is , which is not equal to . Therefore, the lengths of CD and C'D' are not equal
[question 1] Answer
False
[question 2] Answer
False
Key Concept
Dilation and Perimeter
Explanation
When a figure is dilated by a scale factor, the lengths of the sides are multiplied by that factor. This changes the perimeter proportionally to the scale factor.
Key Concept
Dilation and Side Lengths
Explanation
The length of a side after dilation is the original length multiplied by the scale factor. If the scale factor is not 1, the dilated length is different from the original length.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question