
Sia
中文解答,最后结果改为小数
Question 1
Let and .
a)
Calculate v .
b)
What is the angle between and in radians?
Round your answer to 3 decimal places.
All answers saved
2 marks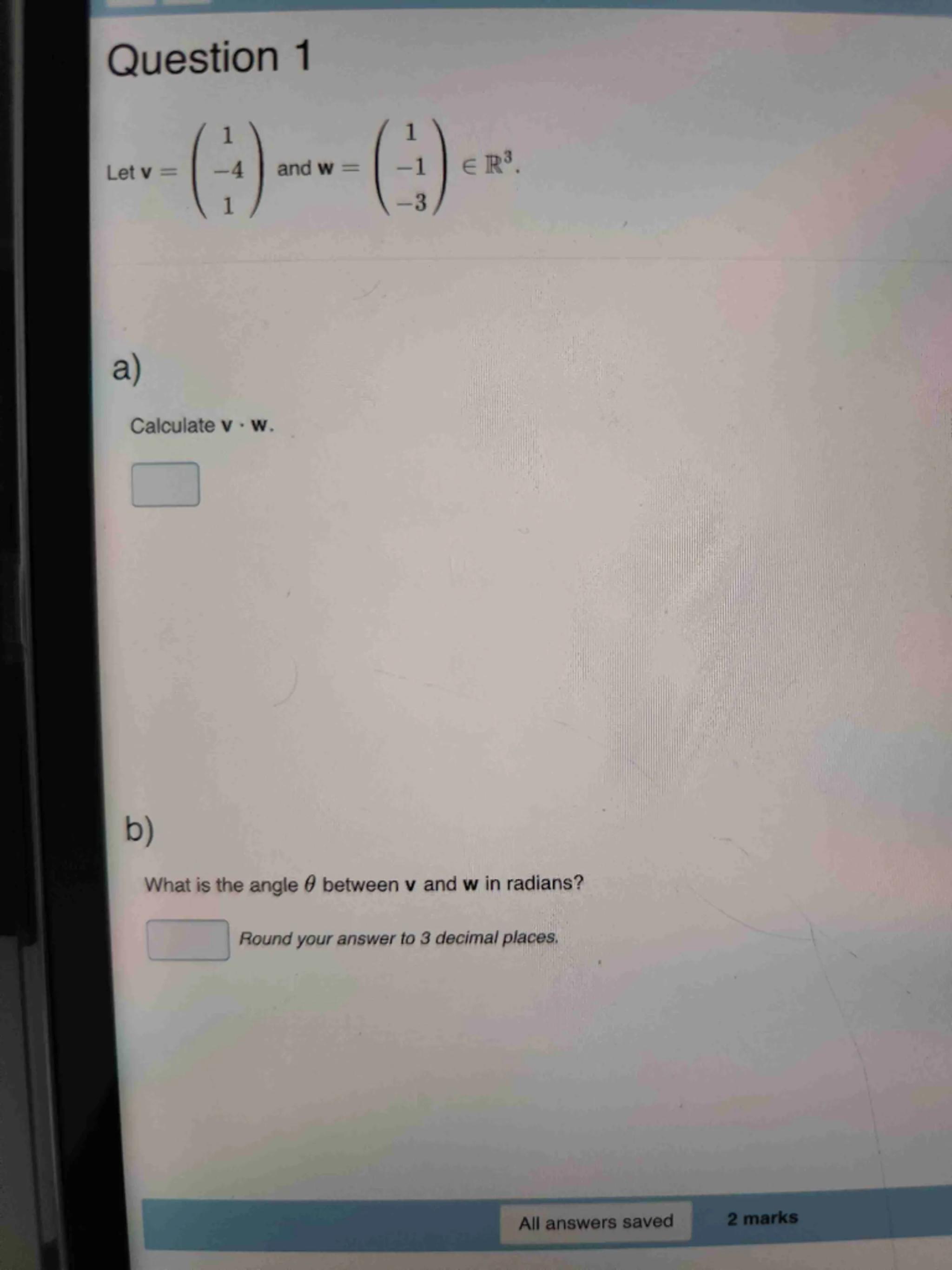

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To calculate the dot product of vectors and , we use the formula:
step 2
Substituting the values, we have:
step 3
Simplifying this gives:
step 4
The angle between the vectors can be calculated using the formula:
step 5
First, we find the magnitudes: and
step 6
Now substituting into the cosine formula:
step 7
Calculating , thus
step 8
Finally, to find , we take the inverse cosine: . Rounding to three decimal places gives the final angle
Answer
Dot product: 2; Angle : [Insert angle in radians rounded to three decimal places]
Key Concept
The dot product and angle between vectors are fundamental concepts in vector algebra.
Explanation
The dot product provides a measure of how parallel two vectors are, while the angle gives insight into their directional relationship.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question
