
Sia

Question
Math
Posted over 1 year ago
Refer to the graph of the function in the following figure.
(a) Find the value of .
(b) Find the values of corresponding to the point(s) on the graph of located at a height of 5 units above the -axis.
(smaller value) (larger value)
(c) Find the point on the -axis at which the graph of crosses it.
What is the value of at this point?
(c) Find the point on the -axis at which the graph of crosses it.
What is the value of at this point?
(d) Find the domain and range of . (Enter your answers using interval notation.) domain
range 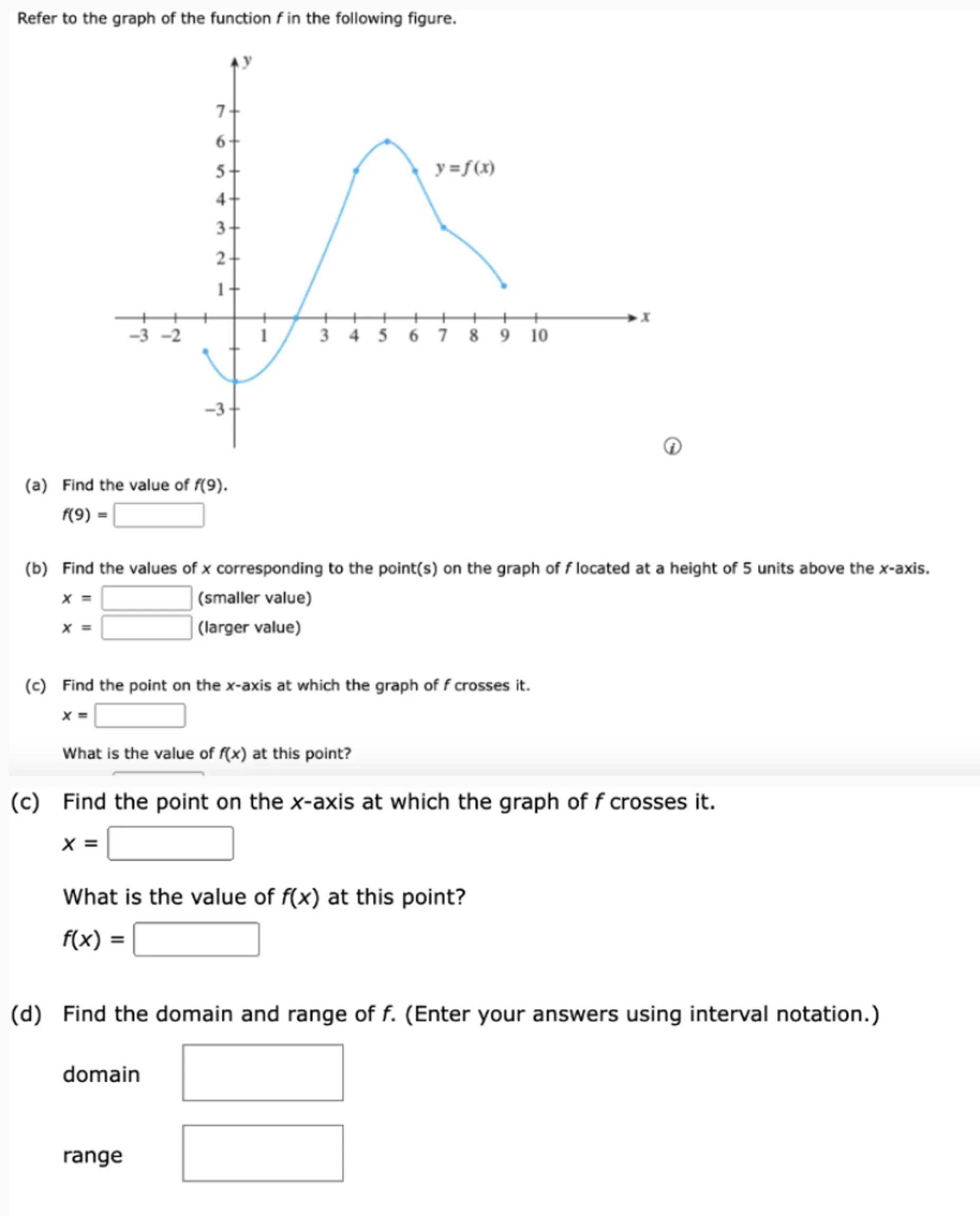

Answer from Sia
Posted over 1 year ago
Solution by Steps
step 1
To find the value of , we look at the graph where . From the graph, we see that the point corresponding to is . Therefore,
step 2
To find the values of corresponding to the point(s) on the graph of located at a height of 5 units above the -axis, we look for points where . From the graph, we see that the points are . Therefore, the smaller value of is and there is no larger value
step 3
To find the point on the -axis at which the graph of crosses it, we look for points where . From the graph, we see that the points are . Therefore,
step 4
The value of at the point where the graph crosses the -axis is
step 5
To find the domain and range of , we observe the graph. The domain is the set of all values for which the function is defined, which is . The range is the set of all values that the function takes, which is
[question number] Answer
A
Key Concept
Graph Analysis
Explanation
To find specific values and points on a graph, observe the coordinates and the behavior of the function as it intersects the axes and reaches certain heights.
Not the question you are looking for? Ask here!
Enter question by text
Enter question by image
Unlock Smarter Learning with AskSia Super!
Join Super, our all-in-one AI solution that can greatly improve your learning efficiency.
30% higher accuracy than GPT-4o
Entire learning journey support
The most student-friendly features
Study Other Question